DIỆN TÍCH HÌNH NÓN – THỂ TÍCH KHỐI NÓN TRÒN XOAY
I. TÓM TẮT LÝ THUYẾT
1. Diện tích xung quanh của hình nón tròn xoay:
Diện tích xung quanh của hình nón tròn xoay bằng một nửa tích của độ dài đường tròn đáy và độ dài đường sinh.
Sxq = π.R.l
2. Diện tích toàn phần
Stp = π.R.l + π.R2 = π.R (l + R)
3. Thể tích khối nón tròn xoay:
Thể tích của khối nón tròn xoay bán kính R và đường cao h là:
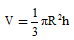
II. PHƯƠNG PHÁP GIẢI BÀI TẬP
Bài 1: Thiết diện qua trục của một hình nón là một tam giác vuông cân SAB có cạnh góc vuông bằng a. Tính diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón tương ứng.
Bài 2: Tính thể tích hình nón biết thể tích hình chóp tam giác đều nội tiếp trong hình nón là V.
Bài 3: Cho tam giác đều ABC có diện tích bằng S quay xung quanh cạnh AC của nó. Tính thể tích khối tròn xoay tạo thành.
Bài 4: Cho hình chóp tứ giác đều có diện tích xung quanh là S. Hình nón nội tiếp hình chóp có góc giữa đường sinh và trục bằng 300. Tính thể tích của khối nón tròn xoay.
Bài 5: Cho khối nón ngoại tiếp tiếp tứ diện đều ABCD. Đỉnh của nón trùng với đỉnh A của tứ diện, đáy của tứ diện là đáy của hình nón. Tính tỉ số thể tích của tứ diện và nón
III. BÀI TẬP TƯƠNG TỰ
Bài 1: Tính thể tích và diện tích xung quanh của khối nón
a. có thiết diện đi qua trục của khối nón là một tam giác vuông cân có cạnh huyền bằng a
b. đỉnh S đường cao SO, A và B là hai điểm thuộc đường tròn đáy hình nón sao cho khoảng cách từ O đến AB bằng a và 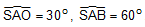
Bài 2. Một hình trụ có hai đáy là hai hình tròn (O; R) và (O’; R); OO’ = RÖ2. Xét hình nón có đỉnh là O’ và đáy là hình tròn (O; R).
a .Tính tỉ số thể tích xung quanh của hình trụ và hình nón.
b. Mặt xung quanh cuả hình nón chia khối trụ thành hai phần, tính tỉ số thể tích của hai phần đó.
Bài 3. Cho một hình cầu bán kính r = 1, nội tiếp một hình nón có chiều cao h và đáy bán kính đáy R
a. Tìm hệ thức liên hệ giữa h và R.
b. Xác định h và R để thể tích hình nón có giá trị nhỏ nhất.
Bài 4. Cho một khối nón đỉnh S, đường cao SO = h, bán kính đáy bằng R; M là một điểm trên đoạn OS, đặt OM = x, 0 < x < h.
a. Tính thể tích của thiết diện (C) khi cắt khối nón bởi mặt phẳng đi qua M và vuông góc với OS.
b. Tính thể tích V của khối nón đỉnh O mà đáy là (C ) theo R và x. Xác định x sao cho V có giá trị lớn nhất.
Bài 5: Cho lục giác đều ABCDEF cạnh a. Tính thể tích hình tròn xoay sinh bởi lục giác đó khi quay quanh:
a. Đường thẳng AD.
b. Đường thẳng đi qua trung điểm của các cạnh AB và DE