Bài 1. Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của BC và BD, M là điểm trên cạnh AD với MD = 3MA. Xác định thiết diện tạo bởi tứ diện ABCD và mặt phẳng (IJM).
Bài 2 (SGK). Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng (ABCD) vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành, d cắt BC tại E.Gọi C’ là một điểm nằm trên cạnh SC.
Tìm thiết diện của hình chóp cắt bởi mặt phẳng (C’AE).
Bài 3. Cho hình chóp S.ABCD có đáy ABCD là tứ giác có AB và CD cắt nhau tại tại một điểm E. M là trung điểm cạnh SC. Xác định thiết diện tạo bởi hình chóp đã cho và mặt phẳng (MAB).
Bài 4. Cho hình chóp S.ABCD.Gọi M, N, P lần lượt là các điểm trên các cạnh SA, SB và BC sao cho MN không song song với SB và NP không song song với CD. Xác định thiết diện tạo bởi (MNP) và hình chóp.
Bài 5. Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC.
a. Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
b. Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN)
c. Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN).
Bài tập đề nghị.
Bài 1. Cho tứ diện ABCD. Trên các đoạn CA, CB, BD cho lần lượt lấy các điểm M, N, P sao cho MN không song song với AB, NP không song song với CD. Gọi (a) là mp xác định bởi ba điểm M, N, P nói trên. Tìm thiết diện tạo bởi (a) và tứ diện ABCD.
Hướng dẫn
Trong mp(ABC), đường thẳng MN cắt AB tại I
Trong mp(ABD), đường thẳng IP cắt AD tại Q.
Ta có: MN =(a)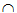 
(ABC)
NP =(a) 
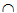(BCD)
PQ =(a)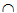(ABD)
QM =(a)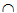(ACD)
Ta được thiết diện cắt tứ diện ABCD bởi mp(a) là tứ giác.
Bài 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, E là ba điểm lần lượt lấy trên AD, CD, SO. Tìm thiết diện của hình chóp với mp (MNE).
Hướng dẫn
Gọi I = MN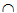BD
Trong mp(SBD): IE cắt SB tại Q
MN cắt BC tại H và MN cắt AB tại K
Ta có: HQ = (SBC)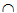(EMN)
Các đoạn MN, NP, PQ, QR, RM là các đoạn giao tuyến của mp(MNE) với đáy và các mặt bên của hình chóp.
Thiết diện là ngũ giác MNPQR.
Bài 3. Cho hình chóp S.ABC. M là một điểm trên cạnh SC, N và P lần lượt là trung điểm của
AB và AD. Tìm thiết diện của hình chóp với mặt phẳng (MNP).
HD: Thiết diện là 1 ngũ giác.
Bài 4.Cho hình chóp S.ABCD, M là một điểm trên cạnh BC, N là một điểm trên cạnh SD.
a. Tìm giao điểm I của BN và (SAC) và giao điểm J của MN và (SAC).
b. DM cắt AC tại K. Chứng minh S, K, J thẳng hàng.
c. Xác định thiết diện của hình chóp S.ABCD với mặt phẳng (BCN).
HD:
a. Gọi O=AC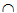BD thì I=SO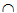BN, J=AIMN
b. J là điểm chung của (SAC) và (SDM)
c. Nối CI cắt SA tại P. Thiết diện là tứ giác BCNP.