VĐ2: TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG
I. Tóm tắt lý thuyết
♦Phương pháp 1:
Muốn tìm giao tuyến của hai mặt phẳng ta có thể tìm hai điểm chung phân biệt của hai mặt phẳng . Khi đó giao tuyến là đường thẳng đi qua hai điểm chung đó.
II. PP GIẢI BÀI TẬP
Bài 1: Cho hình chóp SABCD.Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
Bài 2: Cho hình chóp SABCD có đáy ABCD là hình thang có AB//CD và AB > CD. Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
Bài 3: Cho điểm A không nằm trên mặt phẳng (P) chưa tam giác BCD. Lấy E, F là các điểm lần lượt nằm trên các cạnh AB, AC sao cho EF cắt BC tại I. Tìm giao tuyến của 2 mp(DBC) và (DEF)
Bài 4. (B6 – SGK) Cho bốn điểm A, B, C và D không đồng phẳng. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD. Tìm giao tuyến của hai mặt phẳng (MNP) và (ACD)
Bài 5. Cho tứ diện ABCD. Gọi I, K lần lượt là trung điểm của hai đoạn thẳng AD và BC.
a. Tìm giao tuyến của hai mặt phẳng (IBC) và(KAD)
b. Gọi M, N là điểm trên đoạn AB và AC. Tìm giao tuyến của hai mp (IBC) và (DMN)
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Cho tứ diện ABCD. Lấy O là một điểm thuộc miền trong của tam giác BCD và M là một điểm trên đoạn AO.
a. Tìm giao tuyến của mp(MCD) với các mp(ABC) và (ABD)
b. Gọi I, K là hai điểm lần lượt lấy trên BC và BD. Tìm giao tuyến của mp(IKM) với các mp(ACD), (ABC) và (ABD).
Hướng dẫn
a. Gọi E = BO 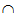 CD
CD
Nối EM cắt AB tại F
Þ Hai mp (MCD) và (ABC) có hai điểm chung là C và F.
Do đó: CF = mp(MCD) 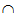 mp(ABC)
mp(ABC)
Hai mp(MCD) và (ABD) có hai điểm chung là D và F
Do đó: DF = mp(MCD)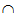 mp(ABD).
mp(ABD).
b. Gọi I’ = IO 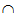 CD
CD
K’ = KO 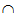 CD
CD
Trong mp(AIO) gọi : H = IM 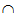 AI’
AI’
Trong mp (AKO) gọi G = KM 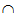 AK’
AK’
Do đó: GH = mp(IKM) 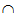 mp(ACD)
mp(ACD)
Gọi P = GH 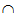 AC; Q = GH
AC; Q = GH 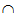 AD
AD
Do đó: IP = mp(IKM) 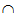 mp(ABC)
mp(ABC)
KQ = mp(IKM) 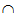 mp(ABD)
mp(ABD)
Bài 2. Cho hình chóp S.ABCD với đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của các đoạn BC, CD, SO. Tìm giao tuyến của mp(MNP) với các mp(SAB), (SAD), (SBC) và (SCD).
Hướng dẫn
Gọi : I = MN cắt AB
G = MN cắt AD.
E = MN 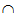 AC
AC
K = EP 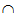 SA
SA
IK = mp(MNP) 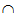 mp(SAB)
mp(SAB)
Tương tự: GK = mp(MNP) 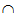 mp(SAD)
mp(SAD)
H = IK cắt SB
MH = mp(MNP) 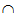 mp(SBC)
mp(SBC)
Tương tự: KG cắt SD tại L
Do đó: LN = mp(MNP) 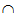 mp(SCD)
mp(SCD)
Ta được thiết diện của hình chóp cắt mp(MNP) là hình ngũ giác MNLKH.