BÀI . PHÉP QUAY
I. TÓM TẮT LÝ THUYẾT
1. Định nghĩa:
Cho điểm O và góc lượng giác α, phép biến hình biến O thành chính nó, biến mỗi điểm M thành M’ sao cho: OM’ = OM và góc lượng giác (OM; OM’) = α được gọi là phép quay tâm O góc α
O: tâm α: góc quay ký hiệu: Q(O; α).
Nếu a = (2k+1)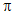
, k 
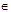Z; phép đối xứng tâm
Nếu a = 2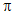k , k 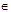Z; phép đồng nhất.
2. Tính chất:
Phép quay là 1 phép dời hình nên nó có đầy đủ tính chất của phép dời hình.
Ngoài ra; d’ = Q(O; α) (d), khi đó:
0 < α≤ 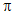/2 : góc giữa d và d’ bằng α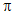/2 <a <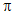: góc giữa d và d’ bằng ( 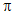– a)
II. PHƯƠNG PHÁP GIẢI BÀI TẬP
VĐ 1: Tìm ảnh qua 1 phép quay.
Bài 1. Cho hình vuông ABCD tâm O. M; N là trung điểm AB, OA. Tìm ảnh của DAMN qua phép quay tâm O, 900.
Bài 2. Trong mặt phẳng Oxy, A(3; 4). Tìm tọa độ điểm A’ là ảnh của A qua phép tâm O góc 900.
Bài 3. Trong mặt phẳng Oxy, cho điểm M(x; y) tìm ảnh M’ qua phép quay tâm O góc a.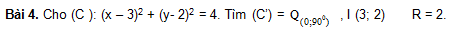 
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Trong mặt phẳng Oxy cho phép quay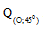 
. Tìm ảnh của :
a. Điểm M(2;2)
b. Đường tròn (C): (x – 1)2 + y2 = 4
Đáp án
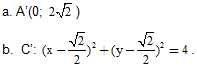
Bài 2. Trong mặt phẳng Oxy cho đường thẳng (D): 2x – y + 1 = 0. Tìm ảnh của đường thẳng qua:
a . Phép đối xứng tâm I (1; -2)
b. Phép quay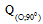 
Đáp án
a . (D’): 2x – y – 9 = 0
b. (D’): x + 2y + 1 = 0.
Bài 3. Trong mặt phẳng tọa độ Oxy, cho điểm M(4; 1).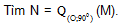 
Đáp án: N(1; -4) hay N(-1; 4)
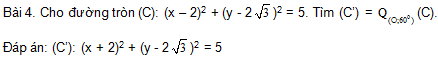
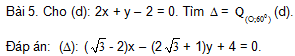
Bài 7. Cho đường thẳng d và điểm O cố định không thuộc d, M là điểm di động trên d. Hãy tìm tập hợp các điểm N sao cho DOMN đều
Bài 8. Chứng minh rằng các đoạn thẳng nối tâm các hình vuông dựng trên các cạnh của một hình bình hành về phía ngoài, hợp thành một hình vuông.
Đáp án
