Bài 1: Cho hình chóp SABCD đáy là hình bình hành ABCD,AC cắt BD tại O.Gọi M,N lần lượt là trung điểm của SC,CD.Chứng minh (MNO) // (SAD).
Bài 2. Cho tứ diện ABCD.Gọi I, J, K lần lượt là trọng tâm của các tam giác ABC, ACD, ABD. Chứng minh rằng (IJK) // (BCD).
Bài 3. Cho hai hình vuông ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Trên các đường chéo AC và BF lần lượt lấy các điểm M và N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M và N lần lượt cắt AD và AF tại M’ và N’.
a. Chứng minh (ADF) // (BCE)
b. Chứng minh M’N’ // DF.
c. Chứng minh (DEF) // (MM’N’N) và MN // (DEF)
Bài 4. Trong mặt phẳng (a) cho hình bình hành ABCD, Qua A, B, C lần lượt vẽ bốn đường thẳng a, b, c, d song song với nhau và không nằm trên (a). Trên a, b, c lần lượt lấy ba điểm A’, B’, C’ tùy ý
a .Xác định giao điểm D’ của đường thẳng d với mp(A’B’C’)
b. Chứng minh rằng A’B’C’D’ là hình bình hành.
Bài 5. Hai hình vuông ABCD và ABEF không nằm trong một mặt phẳng và có cạnh chung AB. Lần lượt láy trên hai đường chéo AC và BF hai điểm M, N sao cho AM = BN. Những đường thẳng song song với AB kẻ từ M và N lần lượt kẻ từ M và N lần lượt cắt AD tại M’ và AF tại N’.
a . Chứng minh hai mp (ADF) và (BCE) song song với nhau
b. Chứng minh rằng MN //(CDF)
Bài 6. Cho hình chóp S.ABCD, E = AB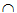
CD, F=AD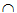BC. Mặt phẳng (P) cắt SA, SB, SC, SD tại I, J,K,L
a .Chứng minh nếu SE//(P) thì IJ//KL
b. Chứng minh IJKL là hình bình hành Û (P)//(SEF)
Bài 7. Trong mp(a) cho hình bình hành ABCD. Ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với (a) lần lượt đi qua các điểm A, B, C, D. Một mp(a’) cắt bốn nữa đường thẳng nối trên tại A’, B’, C’, D’
a .Chứng minh mp(AA’, BB’) //mp(CC’,DD’)
b. Chứng minh tứ giác A’B’C’D’ là hình bình hành
c. Chứng minh AA’+CC’=BB’+DD’
Bài Tập Đề Nghị
Bài 1. Cho tứ diện ABCD. Gọi I, J là hai điểm di động lần lượt trên các cạnh AD, BC sao cho luôn có: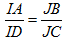 
a. CMR: IJ luôn song song với 1 mặt phẳng cố định.
b. Tìm tập hợp điểm M chia đoạn IJ theo tỉ số k cho trước.
HD:
a. IJ song song với mp qua AB và song song CD.
b. Tập hợp điểm M là đoạn EF với E, F là các điểm chia AB, CD theo tỉ số k.
Bài 2. Cho tứ diện ABCD có AB = AC = AD. CMR các đường phân giác ngoài của các góc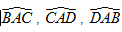 
đồng phẳng.
HD: Cùng nằm trong mặt phẳng qua A và song song với (BCD).
Bài 3. Cho hình chóp S.ABCD có đáy là hình bình hành. Một mặt phẳng (P) cắt các cạnh bên SA, SB, SC, SD lần lượt tại A’, B’, C’, D’. Chứng minh rằng tứ giác A’B’C’D’ là hình bình hành khi và chỉ khi mặt phẳng (P) song song với mp (ABCD).
Hướng dẫn
Giả sử A’B’C’D’ là hình bình hành
Từ đó chứng minh: A’B’//(ABCD)
A’D’//(ABCD)
Þ (P) //(ABCD).
Þ Tứ giác A’B’C’D’ là hình bình hành.
Bài 4. Từ bốn đỉnh của hình bình hành ABCD vẽ bốn nửa đường thẳng song song cùng chiều Ax, By, Cz và Dt sao cho chúng cắt mp(ABCD). Một mặt phẳng (a) cắt bốn nửa đường thẳng theo thứu tự nói trên tại A’, B’, C’ và D’. Chứng minh rằng (Ax,By)//(Cz,Dt) và (Ax, Dt)//(By, Cz).
Hướng dẫn
Ta có: Ax// Dt, Dt Ì(Cz, Dt)
Þ Ax// (Cz, Dt)
AB//CD, CD Ì(Cz, Dt)
Þ AB//(Cz, Dt)
Từ Ax, AB Ì(Ax, By) Þ (Ax, By)//(Cz, Dt)
Tương tự ta có: (Ax, Dt)//(By, Cz)