VĐ1: CHỨNG MINH HAI ĐƯỜNG THẲNG SONG SONG
Bài 1. Cho tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của AB, CD, BC, AD, AC, BD. Chứng minh tứ giác MQNP là hình bình hành.Từ đó suy ra 3 đoạn MN, PQ, RS cắt nhau tại trung điểm mỗi đoạn.
Bài 2. Cho tứ diện ABCD có I, J lần lượt là trọng tâm của các tam giác ABC, ABD. Chứng minh IJ song song với CD.
Bài 3. Cho tứ diện ABCD. Gọi M, N theo thứ tự là trung điểm của AB, BC và Q là một điểm nằm trên cạnh AD và P là giao điểm của CD với mặt phẳng (MNQ). Chứng minh rằng PQ//MN và PQ//AC.
Bài 4. Cho hai hình vuông ABCD và ABEF có chung hai cạnh AB và không cùng nằm trên một mặt phẳng. M trên đường chéo AC và N trên đường chéo BF với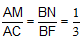 
a. Chứng minh DM, AB và EN đồng quy tại trung điểm I của AB
b. Chứng minh MN song song với DE.
Bài tập đề nghị
Bài 1. Cho tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các đoạn thẳng AB, CD, BC, DA, AC, BD.Chứng minh ba đoạn thẳng MN, PQ và RS đồng quy tại trung điểm G của mỗi đoạn. Điểm G đó gọi là trọng tâm của tứ diện ABCD đã cho.
Hướng dẫn
Vì MP là đường trung bình của tam giác ABC, NQ là đường trung bình của tam giác ADC nên MP // AC, NQ // AC. Vậy MP // NQ và MP = NQ, do đó tứ giác MPNQ là hình bình hành.
Từ đó, ta suy ra các đoạn thẳng MN và PQ cắt nhau tại trung điểm của mỗi đoạn.
Chứng minh tương tự, các đoạn thẳng MN và RS cũng cắt nhau tại trung điểm của mỗi đoạn. Vậy, ba đoạn thẳng MN, PQ, RS đồng quy tại trung điểm G của mỗi đoạn thẳng đó.
Bài 2. Cho tứ diện ABCD, chứng minh hai đường thẳng AB và CD chéo nhau ?
Hướng dẫn
Ta có: CD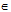 
(BCD)
AB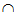 
(BCD) = B
B 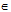CD
Vậy AB và CD chéo nhau
Bài 3. Cho hình chóp tứ giác S.ABCD có AD cắt BC. Hãy tìm điểm M nằm trên cạnh SD và điểm N trên cạnh SD và điểm N trên cạnh SC sao cho AM//BN.
Hướng dẫn
Gọi I là giao điểm của BC và AD. Khi đó: (SAD)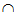(SBC) = SI
Giả sử có M 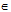SD, N 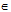SC sao cho AM//BN. Khi đó hai mặt phẳng (SAD) và (SBC) cắt nhau theo giao tuyến SI phải song song với AM và BN. Từ đó ta suy ra cách xác định điểm M và N như sau:
Từ A trong mp(SAD) ta kẻ đường thẳng song song với SI, cắt SD tại M; từ B trong mp(SBC) ta kẻ đường thẳng song song với SI, cắt SC tại N. Khi đó M và N hai điểm cần tìm.
Bài 4. Cho hình chóp tứ giác S.ABCD có đáy là một tứ giác lồi. Gọi M, N, E, F lần lượt là trung điểm của các cạnh bên SA, SB, SC và SD. Chứng minh rằng:
a. ME//AC, NF//BD
b. Ba đường thẳng ME, NF, và SO ( O là giao điểm của AC và BD) đồng quy.
c. Bốn điểm M, N, E, F đồng phẳng.
Hướng dẫn
a. Xét tam giác SAC. Ta có ME là đường trung bình nên ME//AC. Tương tự NF//BD.
b. Trong mp(SAC) gọi I giao điểm ME và SO. I trung điểm SO. FI là đường trung bình của tam giác SOD
Vậy FI//DO.
Gọi N’ là giao điểm của FI với SB
Do FN’//BD và F trung điểm của SD
=> N’ trung điểm của SB, hay N’ºN
Vậy ba đường thẳng ME, NF, SO đồng quy tại I
c. Do ME và NF cắt nhau tại I, nên qua ME và NF xác định một mp. Từ đó suy ra bốn điểm M, N, E, F đồng phẳng.