BÀI 3 : ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG
BÀI TẬP ÁP DỤNG
Bài 1. Cho tứ diện S.ABC có cạnh SA vuông góc với mặt phẳng (ABC) và có ABC là tam giác vuông tại B.
a. Chứng minh BC vuông góc với mặt phẳng (SAB) và BC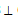 
SB.
b. Gọi AH là đường cao của tam giác SAB. Chứng minh AH 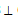SC.
Bài 2. Hình chóp S.ABCD có đáy ABCD là hình vuông và có cạnh SA vuông góc với mặt phẳng đáy (ABCD). Gọi H và K lần lượt là hình chiếu vuông góc của điểm A trên SB và SD.
a. Chứng minh BC 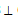(SAB), CD 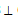(SAD), BD 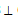(SAC)
b. Chứng minh SC 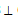(AHK) và HK 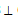(SAC).
Bài 3. Hình chóp S.ABCD có đáy là hình thoi ABCD tâm O và có SA = SC, SB = SD.
a. Chứng minh đường thẳng SO vuông góc với mặt phẳng (ABCD).
b. Gọi M, N lần lượt là trung điểm của SB và SD. Chứng minh MN 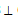(SAC).
Bài 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Gọi H, I, K lần lượt là hình chiếu vuông góc của điểm A trên SB, SC, SD.
a. Chứng minh rằng BC 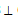mp(SAB), CD 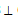mp(SAD), BD 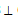mp(SAC).
b. Chứng minh SC 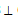mp(AHK) và điểm I cũng thuộc mp(AHK) đó.
c. Chứng minh rằng HK 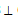mp(SAC) từ đó suy ra HK 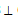AI.
Bài 5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SB = SD.
a. Chứng minh (SAC) là mặt phẳng trung trực của đoạn BD.
b. Gọi H và K lần lượt là hình chiếu vuông góc của A trên SB và SD. Chứng minh : SH = SK, OH = OK và HK // BD.
c. Chứng minh (SAC) là mặt phẳng trung trực của đoạn HK.