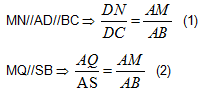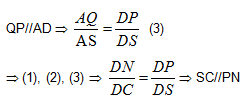VĐ1: Chứng minh đường thẳng song song với mặt phẳng

BÀI TẬP ÁP DỤNG

Bài 1.Cho tứ diện ABCD.G là trọng tâm tam giác ABD. Trên đoạn BC lấy điểm M sao cho MB = 2MC. Chứng minh rằng MG // (ACD)

Bài 2. Cho tứ diện ABCD.Gọi M, N lần lượt là trọng tâm của các tam giác ACD và BAD. Chứng minh rằng MN song song với các mặt phẳng (ABC) và (BDC)

Bài 3. Hai hình bình hành ABCD và ABEF không cùng nằm trong mặt phẳng .

A .Gọi O, O’ lần lượt là tâm hình bình hành ABCD và ABEF . Chứng minh đường thẳng OO’ song song với các mặt (ADF) và (BCE)

b. Gọi M và N  lần lượt là trọng tâm cuả tam giác ABDvà ABE. Chứng minh MN//(CEF).

Bài  4. Cho hình chóp S.ABCD. Gọi M, N lần lượt là trọng tâm của tam giác SAB và ABC. Chứng minh rằng MN//(SCD)

Bài 5. Cho hình hộp ABCD.A’B’C’D’. Gọi M, N theo thứ tự là các trung điểm của các cạnh AD, CC’

A . Chứng minh MN//(ACB’)

b . Xét trường hợp tổng quát khi M, N là hai điểm lấy trên các cạnh AD và CC’ thỏa mãn điều kiện 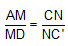. Chứng minh MN//(ACB’)

Bài 6. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm các cạnh AB, CD

a. Chứng minh MN song song với các mặt phẳng (SBC) và (SAD)

b. GỌI P là trung điểm của SA. Chứng minh SB, SC đều song song với (MNP)

c. Gọi G₁ và G₂ là trọng tâm tam giác ABC và SBC. Chứng minh G₁G₂ // (SAB).

Bài Tập Đề Nghị

Bài 1. Cho tứ diện ABCD. Gọi G₁ và G₂ lần lượt là trọng tâm của các tam giác ACD và BCD. Chứng minh rằng G₁G₂ song song với các mặt phẳng (ABC) và (ABD)

Hướng dẫn

Gọi I là trung điểm CD

G₁ trọng tâm của tam giác ACD nên G₁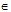AI

G₂ trọng tâm của tam giác BCD nên G₂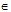BI

ÞG₁G₂ //AB

AB 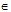(ABC) Þ G₁G₂ //(ABC)

Và AB 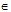(ABD) Þ G₁G₂//(ABD).

Bài 2. Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SAB và I trung điểm của AB. Lấy điểm M trong đoạn AD sao cho AD =3AM.

a. Tìm giao tuyến của hai mp (SAD) và (SBC)

b. Đường thẳng qua M và song song với AB cắt CI tại N. Chứng minh rằng NG//(SCD)

c. Chứng minh rằng MG//(SCD).

Hướng dẫn

a. Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC)

Ta có: AD 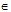(SAD) ,      BC 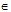(SBC),           AD//BC

Þ (SAD)Ç(SBC) = Sx   và Sx//AD//BC

b. Ta có: MN//IA//CD

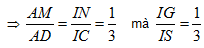
  Þ GN//(SCD).

c. Giả sử IM cắt CD tại K Þ SK 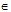(SCD)

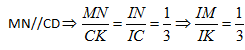
Þ GM//SK Þ GM//(SCD).

Bài 3. Cho hình chóp S.ABCD với ABCD là hình thang đáy lớn là AD. Gọi M là một điểm bất kỳ trên cạnh AB, (a) là mp qua M và song song với AD và SB

a. Mặt phẳng (a) cắt S.ABCD theo thiết diện là hình gì?

b. Chứng minh SC//(a).

Hướng dẫn

a. (a)  và (SAB) có chung nhau điểm M và (a)//SB nên (a) cắt (SAB) theo giao tuyến Mx với Mx//SB. Gọi Q=MxÇSA

Khi đó: (a) và (SAD) có chung nhau điểm Q và (a)//AD nên (a) cắt (SAD) theo giao tuyến Qy với Qy//AD

Gọi P = QyÇSD

Mặt khác: (a) và (ABCD) có chung nhau điểm M và (a)//AD nên (a) cắt (ABCD) theo giao tuyến Mz với Mz//AD.

Gọi N = MzÇCD

Khi đó (a) cắt các mặt của hình chóp theo các đoạn giao tuyến: MN, NP, PQ, QM

Vậy MNPQ là thiết diện phải tìm (MN//PQ)

Þ MNPQ là hình thang.

b. Ta có: