Bài 1: Cho ba điểm A, B, C không thuộc mặt phẳng (Q) và các đường thẳng BC, CA, AB cắt (Q) lần lượt tại M, N, P. Chứng minh rằng M, N, P thẳng hàng.
Bài 2. Cho tứ diện SABC. Trên các cạnh SA, SB, SC lần lượt lấy các điểm D, E, F sao cho DE cắt AB kéo dài tại I, EF cắt BC kéo dài tại J, FD cắt CA kéo dài tại K. Chứng minh rằng 3 điểm I ,J ,K thẳng hàng.
Bài 3. Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến d. Trong (α) lấy hai điểm A và B sao cho AB cắt d tại I. O là một điểm nằm ngoài (α), (β) sao cho OA và OB lần lượt cắt (β) tại A’ và B’.
a. Chứng minh 3 điểm I, A’, B’ thẳng hàng
b. Trong (α) lấy điểm C sao cho A, B, C không thẳng hàng. Gỉasử OC cắt (β) tại C’, BC cắt B’C’ tai J, CA cắt C’A’ tại K. Chứng minh rằng I, J, K thẳng hàng.
Bài 4. Cho bốn điểm A, B, C, D không đồng phẳng . Gọi M, P, Q là các điểm lần lượt thuộc các đoạn AC, BC, CD. Các cặp đường thẳng AP và MB, AQ và MD cắt nhau lần lượt tại E và F. Chứng minh PQ cắt BD tại K thì K, E, F thẳng hàng.
Bài 5. Trong mặt phẳng (a) cho tứ giác ABCD có cạnh đối AD và BC cắt nhau tại N, S là điểm không thuộc mặt phẳng (a). Gọi I là điểm thuộc cạnh SB, E là giao điểm của DI và mặt phẳng (SAC), K là giao điểm của SC và NI. Chứng minh rằng A, E, K thẳng hàng.
BÀI TẬP ĐỀ NGHỊ
Bài 1. Cho tứ diện SABC có D, E lần lượt là trung điểm của AC,BC và G là trọng tâm của tam giác ABC. Mặt phẳng (a) qua AC cắt SE, SB lần lượt tại M, N. Một mặt phẳng (β) qua BC cắt SD, SA lần lượt là tại P và Q.
a. Gọi I = AM ∩DN và J = BP ∩ EQ.Chứng minh bốn điểm S, I, J , G thẳng hàng
b. Giả sử AN ∩ DM = K ; BQ ∩ EP = L.Chứng minh S, K, L thẳng hàng.
Hướng dẫn
a. Ta có S, I, J, G là điểm chung của hai mặt phẳng (SAE) và (SBI) nên chúng thẳng hàng
b. Vì S, K, L là điểm chung của hai mặt phẳng (SAB) và (SDE) nên chúng thẳng hàng.
Bài 2. Cho hình chóp S.ABCD. Gọi I là một điểm trên cạnh AD và K là một điểm trên cạnh SB.
a . Tìm giao điểm E, F của IK và DK với mp(SAC)
b . Gọi O = AD∩ BC, M = SC∩ OK. Chứng minh bốn điểm A, E, F, M thẳng hàng.
Hướng dẫn
a. Gọi H = AC∩ BI; G = AC∩ BD
Trong mp(SBI): IK cắt SH tại E
Trong mp(SBD): DK cắt SG tại F
Ta có: E = IK ∩ mp(SAC); F = DK ∩ mp(SAC).
b. Các điểm A, E, F, M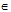 
mp(AKO)
Các điểm A, E, F, M 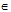mp(SAC)
Vậy A, E, F, M là bốn điểm chung của hai mp(AKO) và (SAC) nên chúng cùng nằm trên đường giao tuyến của hai mp đó
Vì vậy chúng thẳng hàng.