BÀI 4. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG
I. TÓM TẮT LÝ THUYẾT
Vị trí tương đối của hai đường thẳng
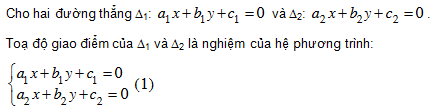
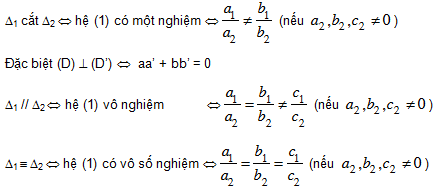
Để chứng minh ba đường thẳng đồng qui, ta có thể thực hiện như sau:
– Tìm giao điểm của hai trong ba đường thẳng.
– Chứng tỏ đường thẳng thứ ba đi qua giao điểm đó.
II. BÀI TẬP ÁP DỤNG
Bài 1. Nhận xét gì về những đường thẳng sau:
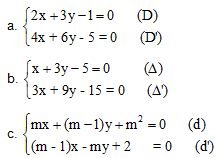
Bài 2. Cho hai đường (D): mx – (m + 2)y + m – 2 = 0
(D’): (3m – 2)x – (5m – 2)y + (7m – 6) = 0
Định m để (D) và (D’):
a. Cắt nhau; b. Trùng nhau; c. Song song.
Bài 3. Cho hai đường thẳng d và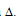 
. Tìm m để hai đường thẳng:
i) cắt nhau ii) song song iii) trùng nhau
a. d: 2mx + (m -1)y – 2 = 0, 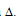: (m + 2)x + (2m +1)y – (m + 2) = 0
b. d: (m – 2)x + (m – 6)y + m -1 = 0 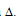: (m – 4)x + (2m – 3)y + m – 5 = 0
Bài 4. Tìm m để ba đường thẳng sau đồng qui:
a. y = 2x – m, y = -x + 2m, mx – (m – 1)y = 2m -1
b. 5x + 11y = 8, 10x – 7y = 74, 4mx + (2m -1)y = m + 2
Bài 5. Viết phương trình đường thẳng d đi qua giao điểm của hai đường thẳng d1 và d2 và:
a. d1: 3x – 5y + 2 = 0, d2: 5x – 2y + 4 = 0, d song song d3: 2x – y + 4 = 0
b. d1: 3x – 2y + 5 = 0, d2: 2x + 4y – 7 = 0, d vuông góc d3: 4x – 3y + 5 = 0
Bài 5. Tìm điểm mà các đường thẳng sau luôn đi qua với mọi m:
a. mx – y + (2m + 1) = 0.
b. mx – y – 2m – 1 = 0.
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Xét vị trí tương đối của các cặp đường thẳng sau, nếu chúng cắt nhau thì tìm toạ độ giao điểm của chúng:
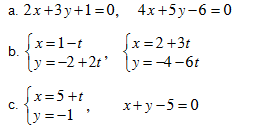
Bài 2. Cho hai đường thẳng d và 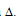. Tìm m để hai đường thẳng:
i) cắt nhau ii) song song iii) trùng nhau
a. d: mx – 5y + 1 = 0 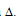: 2x + y – 3 = 0
b. d: (m + 3)x + 2y + 6 = 0 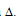: mx + y + 2 – m = 0
Bài 3. Tìm m để ba đường thẳng sau đồng qui:
a. y = 2x – 1, 3x + 5y = 8, (m + 8)x – 2my = 3m
b. 3x – 4y + 15 = 0, 5x + 2y – 1 = 0, mx – (2m – 1)y + 9m – 13 = 0
Bài 4. Viết phương trình đường thẳng d đi qua giao điểm của hai đường thẳng d1 và d2 với:
d1: 3x – 2y + 10 = 0, d2: 4x + 3y – 7 = 0, d qua A(2; 1).