BÀI 10. VỊ TRÍ TƯƠNG ĐỐI GIỮA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
I. TÓM TẮT LÝ THUYẾT
Để biện luận số giao điểm của đường thẳng d: Ax + By + C = 0 và đường tròn (C): x2 + y2 + 2ax + 2by + c = 0, ta có thể thực hiện như sau:.
- Cách 1: So sánh khoảng cách từ tâm I đến d với bán kính R.
– Xác định tâm I và bán kính R của (C).
– Tính khoảng cách từ I đến d.

- Cách 2: Toạ độ giao điểm (nếu có) của d và (C) là nghiệm của hệ phương trình:
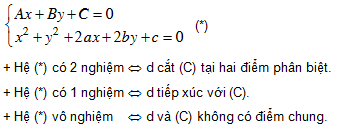
II. BÀI TẬP ÁP DỤNG
Bài 1. Khảo sát vị trí tương đối giữa đường tròn (C): x2 + y2+ 6x + 4y + 9 = 0
và đường thẳng (D) º x – y + 2 = 0.
Bài 2. Cho đường tròn (C): x2 + y2– 2x + 4/5 = 0 và đường thẳng di động (Dm): mx – y – 2m + 3 = 0. Biện luận theo m vị trí tương đối giữa (C) và (Dm).
Bài 3. Biện luận theo m số giao điểm của đường thẳng d và đường tròn (C), với:
d: x + y – 1 = 0, (C): x2 + y2 – 2(2m + 1)x – 4y + 4 – m = 0
Bài 4. Cho đường tròn (C): x2 + y2 – 2x – 2y + 1 = 0 và đường thẳng d đi qua điểm A(–1; 0) và có hệ số góc k
a. Viết phương trình đường thẳng d.
b. Biện luận theo k vị trí tương đối của d và (C).
c. Suy ra phương trình các tiếp tuyến của (C) xuất phát từ A.
Bài 5. Cho đường thẳng d và đường tròn (C): chứng tỏ d cắt (C) và tìm toạ độ các giao điểm của d và (C).
a. d đi qua M(–1; 5) và có hệ số góc k = -1/3, (C): x2 + y2 – 6x – 4y + 8 = 0
b. d: 3x – y – 10 = 0, (C): x2 + y2 – 4x – 2y – 20 = 0
III. BÀI TẬP ÁP DỤNG
Bài 1. Biện luận theo m số giao điểm của đường thẳng d và đường tròn (C), với:
a. d: 2x – y + m = 0, (C): x2 + y2 – 6x + 2y + 5 = 0
b. d: mx + y – 4m = 0, (C): x2 + y2 – 2x – 4y – 4 = 0
Bài 2. Cho đường thẳng d và đường tròn (C): chứng tỏ d cắt (C) và tìm toạ độ các giao điểm của d và (C).
d: 3x – y – 10 = 0, (C): x2 + y2 – 4x – 2y – 20 = 0