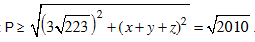BÀI 5. ỨNG DỤNG BẤT ĐẲNG THỨC TÌM GTLN VÀ GTNN
I. TÓM TĂT LÝ THUYẾT
II. BÀI TẬP ÁP DỤNG
Bài 1. Tìm GTLN-GTNN của các hàm số sau
a. y = (x + 3)(5 – x) (-3 ≤ x ≤ 5)
b. y = (x + 1)(2 – x) (-1 ≤ x ≤ 2)
c. y = (2x – 3)(6 – 2x) (3/2 ≤ x ≤ 3)
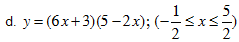
Bài 2. Tìm GTNN của các hàm số sau
a. y = 2x + 1/2x ( x > 0)
b. y = x + 3 + 1/(x + 3) (x > -3)
c. y = 2x +36/(2x – 4) ( x > 2)
Bài 3. Áp dụng BĐT Cô–si để tìm GTNN của các biểu thức sau:

Bài 4. Áp dụng BĐT Cô–si để tìm GTNN của các biểu thức sau:

Bài 5.
a. Tìm GTLN của biểu thức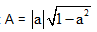
b. Tìm GTNN của hàm số: 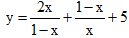 với 0 < x < 1.
với 0 < x < 1.
c. Tìm GTLN của biểu thức: 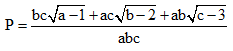 với a ≥ 1, b ≥ 2, c ≥ 3
với a ≥ 1, b ≥ 2, c ≥ 3
d. Tìm GTLN của biểu thức 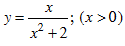
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Áp dụng BĐT Cô–si để tìm GTLN của các biểu thức sau:
a. y = (x + 3)(5 – x); -3 ≤ x ≤ 5. b. y = x(6 – x); 0≤ x ≤ 6
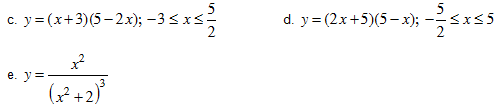
HD: a. Maxy = 16 khi x = 1 b. Maxy = 9 khi x = 3
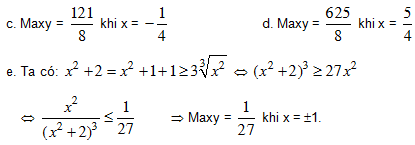
Bài 2. Cho a, b, x, y 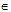 R. Chứng minh bất đẳng thức sau (BĐT Min–cốp–xki):
R. Chứng minh bất đẳng thức sau (BĐT Min–cốp–xki):
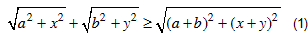
Áp dụng chứng minh các bất đẳng thức sau:
a. Cho a, b ≥ 0 thoả a + b = 1. Tìm GTNN của : 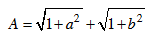 .
.
b. Tìm GTNN của biểu thức 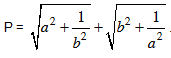 .
.
HD: Bình phương 2 vế ta được: (1) 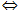
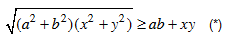 (*)
(*)
Nếu ab + xy < 0 thì (*) hiển nhiên đúng.
Nếu ab + xy ≥ 0 thì bình phương 2 vế ta được: (*) 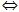 (bx – ay)2 ≥ 0 (đúng).
(bx – ay)2 ≥ 0 (đúng).
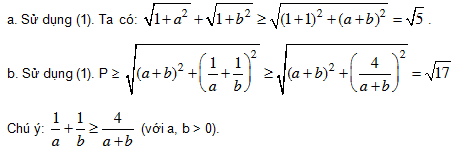
Bài 3.
a. Cho x, y, z > 0 thoả mãn x + y + z = 1. Chứng minh:
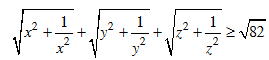
b. Cho x, y, z > 0 thoả mãn x + y + z = 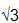 . Tìm GTNN của biểu thức:
. Tìm GTNN của biểu thức:
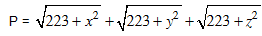
HD: a. Áp dụng (1) liên tiếp hai lần ta được:
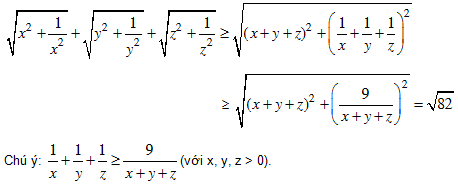
b. Tương tự câu a). Ta có