BÀI 11. PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐƯỜNG TRÒN
I. TÓM TẮT LÝ THUYẾT
Dạng 1: Tiếp tuyến tại một điểm M0(x0, y0) thuộc đường tròn.
Ta dùng công thức tách đôi tọa độ.
– Nếu phương trình đường tròn là:
x2 + y2– 2ax – 2by + c = 0 thì phương trình tiếp tuyến là: xx0 + yy0– a(x + x0) – b(y + y0) + c = 0
– Nếu phương trình đường tròn là:
(x – a)2 + (y – b)2 = R2 thì phương trình tiếp tuyến là:
(x – a)(x0– a) + (y – b)(y0– b) = R2 (h.73)
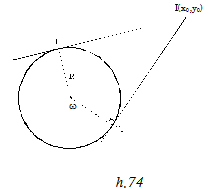
Dạng 2:Tiếp tuyến vẽ từ một điểm I(x0, y0) cho trước ở ngoài đường tròn.
Viết phương trình của đường 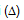 qua I(x0, y0):
qua I(x0, y0):
y – y0 = m(x – x0) 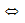 mx – y – mx0 + y0 = 0 (1)
mx – y – mx0 + y0 = 0 (1)
Cho khoảng cách từ tâm I của đường tròn (C) tới 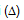 bằng R, ta tính được m; thay m vào (1) ta được phương trình tiếp tuyến.
bằng R, ta tính được m; thay m vào (1) ta được phương trình tiếp tuyến.
* Ghi chú: Ta luôn luôn tìm được hai đường tiếp tuyến. (h. 74)
Dạng 3: Tiếp tuyến 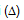 song song với một phương cho sẵn có hệ số góc k.
song song với một phương cho sẵn có hệ số góc k.
Phương trình của  có dạng:
có dạng:
y = kx + m (m chưa biết)  kx – y + m = 0
kx – y + m = 0
Cho khoảng cách từ tâm I đến (D) bằng R, ta tìm được m.
* Ghi chú: Ta luôn luôn tìm được hai đường tiếp tuyến (h.75)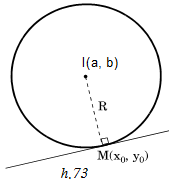
II. BÀI TẬP ÁP DỤNG
Bài 1. Kiểm lại rằng điểm M0(1, –2) ở trên đường (C) có phương trình:
x2 + y2– 10x + 4y + 13 = 0. Tìm phương trình tiếp tuyến với (C) tại M0.
Bài 2. Viết phương trình tiếp tuyến với đường tròn (C): x2 + y2– 4x – 3y = 0 phát xuất từ A(–3, –1).
Bài 3. Cho đường tròn (C) có phương trình: x2 + y2– 6x + 2y + 5 = 0. Tìm phương trình tiếp tuyến với (C) có hệ số góc là –2; định rõ tọa độ các tiếp điểm.
Bài 4. Cho đường tròn (C), điểm A và đường thẳng d.
(C): x2 + y2 + 4x – 8y + 10 = 0, A(2; 2), d: x + 2y – 6 = 0
a. Chứng tỏ điểm A ở ngoài (C).
b. Viết phương trình tiếp tuyến của (C) kẻ từ A.
c. Viết phương trình tiếp tuyến của (C) vuông góc với d.
d. Viết phương trình tiếp tuyến của (C) song song với d.
Bài 5. Cho đường tròn (C): x2 + y2 – 6x – 2my + m2 + 4 = 0.
a. Tìm m để từ A(2; 3) có thể kẻ được hai tiếp tuyến với (C).
b. Viết phương trình các tiếp tuyến đó khi m = 6.
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Cho đường tròn (C) và đường thẳng d:
(C): x2 + y2 – 6x – 2y + 5 = 0, d: 2x – y + 3 = 0
a. Viết phương trình các tiếp tuyến của (C) tại các giao điểm của (C) với các trục toạ độ.
b. Viết phương trình tiếp tuyến của (C) vuông góc với d.
c. Viết phương trình tiếp tuyến của (C) song song với d.
Bài 2. Cho đường tròn (C), điểm A và đường thẳng d.
(C): x2 + y2 – 4x – 6y – 12 = 0, A(-7; 7), d: 3x + 4y – 6 = 0
a. Chứng tỏ điểm A ở ngoài (C).
b. Viết phương trình tiếp tuyến của (C) kẻ từ A.
c. Viết phương trình tiếp tuyến của (C) vuông góc với d.
d. Viết phương trình tiếp tuyến của (C) song song với d.
Bài 3. Cho hai điểm A(1; 2), B(3; 4) và đường thẳng d: y = -3 – 3x
a. Viết phương trình các đường tròn (C1) và (C2) qua A, B và tiếp xúc với d.
b. Viết phương trình tiếp tuyến chung (khác d) của hai đường tròn đó.