BÀI 7. PHƯƠNG TRÌNH ĐƯỜNG TRÒN
1. Phương trình đường tròn
Đường tròn tâm I(a, b) bán kính R có phương trình là:
(x – a)2 + (y – b)2 = R2 (1)
hay: x2 + y2– 2ax – 2by + c = 0 (2)
với c = a2 + b2– R2
Phương trình đường tròn tâm I(a; b), bán kính
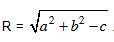 .
.
Ghi chú:
1. Trong phương trình (2):
Hệ sốc = a2 + b2– R2Û R2 = a2 + b2– c ³ 0, đây là điều kiện giữa các hệ số a, b, c để (2) là phương trình của một đường tròn tâm I(a, b) bán kính R.
2. Phương trình đường tròn có những đặc điểm:
– Là phương trình bậc hai đối với x và y.
– Các hệ số của x2 và y2 bằng nhau.
– Không chứa thừa số xy.
Thí dụ: Phương trình của đường tròn (C) tâm I(3, –2) bán kính R = 5 là:
(x – 3)2 + (y + 2)2 = 52Û x2 + y2– 6x + 4y – 12 = 0
Những trường hợp đặc biệt:
Trường hợp 1. Đường tròn có tâm là gốc tọa độ:
Trong trường hợp này ta có:
a = b = 0. Phương trình (1) trở thành: x2 + y2 = R2
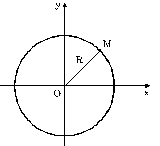
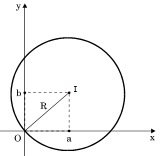
Trường hợp 2. Đường tròn đi qua gốc tọa độ:
Trong trường hợp này ta có: R2 = a2 + b2
Þ c = a2 + b2– R2 = 0
Phương trình (2) có thể viết: x2 + y2– 2ax – 2by = 0
Đây là đường tròn đi qua gốc tọa độ bán kính:
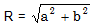
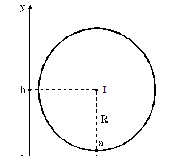
Trường hợp 3. Đường tròn tiếp xúc với hai trục tọa độ:
– Tiếp xúc với trục hoành:
Khi đường tròn (C) tâm I(a, b) tiếp xúc với trục hoành tại điểm A(a, 0), ta có bán kính R =
Phương trình (1) có dạng:
(x – a)2 + (y – b)2– b2 = 0
Û x2 + y2– 2ax – 2by + a2 = 0
Û (x – a)2 + y2– 2by = 0
– Tiếp xúc với trục tung:
Tương tự, khi đường tròn (C) tiếp xúc với trục Oy tại B(b, 0), ta có phương trình:
x2 + y2– 2by + b2 = 0
Û x2 + (y – b)2– 2ax = 0
Trường hợp 4. Đường tròn xác định bởi một đường kính:
– Tâm I là trung điểm của AB.
– Bán kính 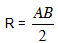 .
.