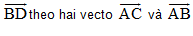PHÂN TÍCH MỘT VECTO THÀNH HAI VECTO KHÔNG CÙNG PHƯƠNG
I. TÓM TẮT LÝ THUYẾT
PP: Sử dụng định lý mọi vectơ đều phân tích được thành 2 vectơ không cùng phương.
Sử dụng quy tắc tam giác, quy tắc hình bình hành trong phép cộng vectơ, quy tắc 3 điểm trong phép trừ 2 vectơ
II. PP GIẢI BÀI TẬP
B1 (B2-SGK) Cho AK và BM là hai trung tuyến của tam giác ABC.Hãy phân tích các vectơ AB, BC, AC theo 2 vectơ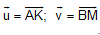 
.
B2 (B3-SGK). Trên đường thẳng chứa cạnh BC của tam giác ABC, lấy một điểm M sao cho vectơ MB = 3 MC. Hãy biểu diễn vectơ AM theo hai vectơ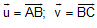 
.
B3. Cho tứ giác ABCD, trên các cạnh AB và CD lần lượt lấy các điểm M, N sao cho: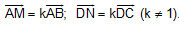 
Hãy phân tích vectơ MN theo hai vectơ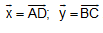 
.
B4. Cho tam giác ABC. Gọi M là trung điểm của AB, D là trung điểm của BC, N là điểm thuộc AC sao cho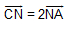 
. K là trung điểm của MN. Chứng minh: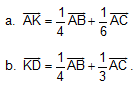
B5. Cho hình bình hành ABCD, đặt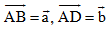 
.Gọi I là trung điểm của CD, G là trọng tâm của tam giác BCI. Phân tích các vectơ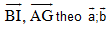 
B6. Cho lục giác đều ABCDEF. Phân tích các vectơ 
B7. Cho hình bình hành ABCD, M là một điểm trên cạnh BC sao cho MB = 3MC
a.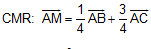 
.
b. Gọi N là điểm trên cạnh CD thỏa ND = 2 CN. Tính các vectơ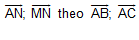
III. BÀI TẬP ĐỀ NGHỊ
B1. Cho hình thang OABC, AM là trung tuyến của tam giác ABC. Hãy phân tích vectơ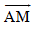 
theo các vectơ 
.
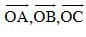B2. Cho DABC. Gọi A1, B1, C1 lần lượt là trung điểm của BC, CA, AB.
a. Chứng minh: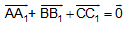 
.
b. Đặt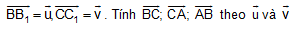 
B3. Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O.
a. Biễu diễn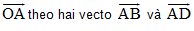 
b. Biễu diễn 