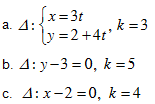BÀI 6. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG
I. TÓM TẮT LÝ THUYẾT
Khoảng cách từ một điểm đến một đường thẳng
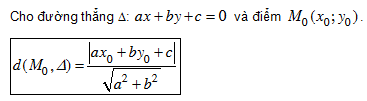
Vị trí tương đối của hai điểm đối với một đường thẳng
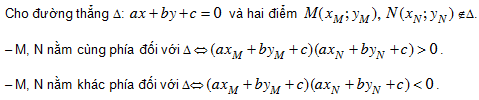
Phương trình các đường phân giác của các góc tạo bởi hai đường thẳng
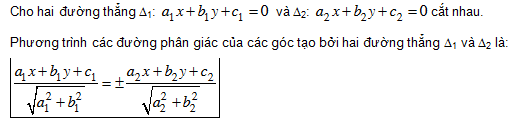
II. BÀI TẬP ÁP DỤNG
Bài 1.
a. Tìm khoảng cách từ điểm M(1, 2) đến đường thẳng
(D) : 4x + 3y – 2 = 0.
b. Tìm khoảng cách từ điểm M(2, 4) đến đường thẳng
(D) : 3x – 2y + 1 = 0
Bài 2. Tìm những điểm nằm trên đường thẳng: 2x + y – 1 = 0 và có khoảng cách đến (D): 4x + 3y – 10 = 0 bằng 2
Bài 3. Viết phương trình của đường thẳng đi qua điểm A(1, –3) và có khoảng cách đến điểm M0(2, 4) bằng 1.
Bài 4. Tìm khoảng cách giữa hai đường thẳng song song:
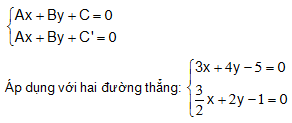
Bài 5. Viết phương trình của đường thẳng (D) song song với (D’):
3x + 4y – 1 = 0 và cách (D’) một đoạn bằng 2.
Bài 6. Tìm bán kính của đường tròn tâm C(–1, –2) và tiếp xúc với đường thẳng: 5x + 12y – 10 = 0.
Bài 7. Cho điểm A(–1, 2) và hai đường (D) º x – y – 1 = 0,
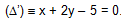. Tìm trên đường thẳng (D) một điểm M sao cho khoảng cách từ M đến (D’) bằng AM.
Bài 8. Tìm phương trình của đường thẳng cách điểm M(1, 1) một khoảng bằng 2 và cách điểm M’(2, 3) một khoảng bằng 4.
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Tính khoảng cách từ điểm M đến đường thẳng d, với:
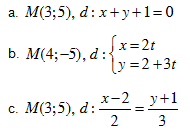
Bài 2.
Bài 3. Cho tam giác ABC. Tính diện tích tam giác ABC, với: A(–2; 14), B(4; –2), C(5; –4)
Bài 4. Viết phương trình đường thẳng d song song và cách đường thẳng D một khoảng k, với:
