B10. Hệ thức lượng trong tam giác vuông – Giải tam giác vuông

HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG

I. TÓM TẮT LÝ THUYẾT

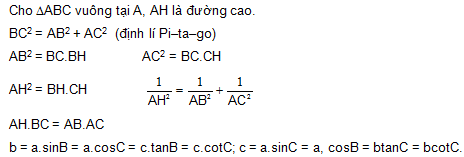
II. PP GIẢI BÀI TẬP

Bài 1. Cho DABC vuông ở A, BC = a, đường cao AH.

a. Chứng minh: AH = a.sinB.cosB, BH = a.cos²B, CH = a.sin²B.

b. Từ đó suy ra AB² = BC.BH, AH² = BH.HC..

Bài 2. Cho DABC vuông tại A, đường cao AH. Biết AB = 7, AC = 9, tính AH, BH, CH

Bài 3. Cho DABC vuông tại A có AB/AC = Ö3. Biết BC = 10. Tính AB, AC

Bài 4. Cho DABC vuông tại C có AB = 5, góc ABC = 60⁰. Tính độ dài đường cao CH và HA.

Bài 5. Cho DABC vuông tại B có AB = a, góc ACB = 60⁰_. Tính độ dài đường cao BH, AH.

Bài 6. Cho DABC vuông tại C có đường cao CH = a, BH = aÖ3. Tính độ dài AC, AH.

III. BÀI TẬP ĐỀ NGHỊ

Bài 1. Cho DABC vuông tại A, đường cao AH. Biết BH = 4, CH = 9, tính AH, AB, AC

Bài 2. Cho DABC vuông tại A có AB = 3, AC = 4. Tính độ dài đường cao AH, góc ABC.

Bài 3. Cho DABC vuông tại A có AH là đường cao, AM là trung tuyến. Biết AM = 4, góc ABC = 30⁰. Tính AH diện tích DABC.