CHỨNG MINH HAI VECTO VUÔNG GÓC, ĐIỀU KIỆN VUÔNG GÓC

I. TÓM TẮT LÝ THUYẾT

ĐK để 2 vecto vuông góc là tích vô hướng bằng 0

Công thức hình chiếu

II. PP GIẢI BÀI TẬP

Bài 1. Chứng minh rằng điều kiện cần và đủ để tam giác ABC vuông tại A là: .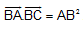

Bài 2. Cho tứ giác ABCD.

a. Chứng minh AB² – BC² + CD² – DA² = 2.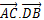

b. Suy ra điều kiện cần và đủ để tứ giác có hai đường chéo vuông góc là: AB² + CD² = BC² + DA².

Bài 3: Cho hình thang vuông ABCD, đường cao AD= h, cạnh đáy AB = a, CD = b. Tìm hệ thức liên hệ giữa a, b, h sao cho:

a. AC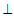BD              b. BD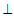AN, với AM là trung tuyến của DABC

Bài 4. Cho DABC cân tại A, O là tâm đường tròn ngoại tiếp. Gọi D là trung điểm của AB và E là trong tâm DACD. CMR OE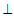CD

Bài 5. Cho 2 vecto 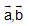  với 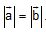. Tìm góc giữa chúng biết rằng .

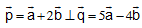III. BÀI TẬP ĐỀ NGHỊ

Bài 1 Cho  ∆ABC  vuông  tại A có AB = c, AC = b. Tìm điểm D trên AC sao cho  BD⊥AM , với AM là trung tuyến của  ∆ABC.

Bài 2 Cho tứ giác ABCD có 2 đường chéo AC và BD vuông góc với nhau tại M và P là trung điểm cuả AD. Chứng minh .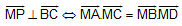

Bài 3. Cho DABC nội tiếp đường tròn tâm O. Gọi BH và CK lần lượt là đường cao của DABC. CMR OA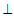HK