B11. Chứng minh các hệ thức lượng trong tam giác

CHỨNG MINH CÁC HỆ THỨC TRONG TAM GIÁC

I. TÓM TẮT LÝ THUYẾT

Chứng minh vế trái bằng vế phải sử dụng các kiến thức:

+ Định lý hàm số Cos, định lý hàm số Sin

+ Độ dài đường trung tuyến, công thức tính diện tích

+ Hệ thức lượng trong tam giác vuông

+ Tính chất của vectơ, tích vô hướng của 2 vectơ

II. PP GIẢI BÀI TẬP

  Bài 1. Cho tam giác ABC có b + c = 2a. CMR:

   a. 2sinA = sinB + sinC

.

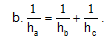   c. 6Rr = bc

  Bài 2. CMR trong tam giác ABC ta có các hệ thức:

a. a = bcosC + ccosB

b. sinA = sinB.cosC + sinCcosB

c. h_a = 2RsinBsinC

d. b² – c² = a(bcosC – cCosB)

  Bài 3. CMR trong tam giác ABC ta có các hệ thức:

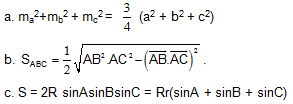
  Bài 5. Cho tam giác ABC. Chứng minh rằng:

a. Nếu bc = a² thì sinB.sinC = sin²A, h_bh_c = h²_a.

b. A vuông Û m²_b + m²_c = 5m²_a.

  Bài 6. Cho DABC vuông ở A, BC = a, đường cao AH.

a) Chứng minh: AH = a.sinB.cosB, BH = a.cos²B, CH = a.sin²B.

b) Từ đó suy ra AB² = BC.BH, AH² = BH.HC.

III. BÀI TẬP ĐỀ NGHỊ

Bài 1. Gọi S là diện tích tam giác ABC. CMR: S = 2R².sinA.sinB.sinC

Bài 2. Gọi S là diện tích tam giác ABC. CMR: S = p(p-a)tg(A/2)

Bài 3. Cho tam giác ABC, CMR (b + c)sinA = a(sinB + sinC)