CHỨNG MINH CÁC ĐẲNG THỨC VECTO
I. TÓM TẮT LÝ THUYẾT
Để chứng minh một đẳng thức vectơ, ta thường sử dụng:
– Qui tắc ba điểm để phân tích các vectơ.
– Các hệ thức thường dùng như: hệ thức trung điểm, hệ thức trọng tâm tam giác.
– Tính chất của các hình.
II. PP GIẢI BÀI TẬP
B1. Cho 6 điểm A, B, C, D, E, F. Chứng minh: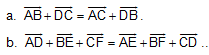
B2. Cho tam giác ABC, có AM là trung tuyến. I là trung điểm của AM.
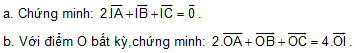
B3. Cho 4 điểm A,B,C,D. Gọi I, J lần lượt là trung điểm của AB và CD. Chứng minh:

d. Gọi P, Q lần lượt là trung điểm của AC và BD; M, N lần lượt là trung điểm của AD và BC . Chứng minh các đoạn thẳng IJ, PQ, MN có chung trung điểm.
B4. Cho 4 điểm A, B, C, D. Gọi I, J lần lượt là trung điểm của BC và CD. Chứng minh: 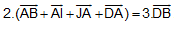 .
.
B5. Cho DABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh: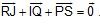 .
.
B6. Cho DABC có M là trung điểm của BC, G là trọng tâm, H là trực tâm, O là tâm đường tròn ngoại tiếp. Chứng minh:
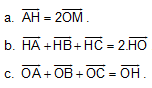
B7. Cho tam giác ABC. Gọi M là điểm trên cạnh BC sao cho MB=2MC. Chứng minh: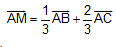 .
.
B8. Cho hình thang OABC. M, N lần lượt là trung điểm của OB và OC. Chứng minh rằng:
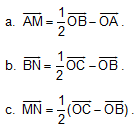
III. BÀI TẬP ĐỀ NGHỊ
B1. Cho DABC. Gọi I là điểm trên cạnh BC sao cho 2CI = 3BI. Gọi F là điểm trên cạnh BC kéo dài sao cho 5FB = 2FC.
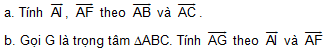
B2. Cho DABC có trọng tâm G. Gọi H là điểm đối xứng của G qua B.
a. Chứng minh: .
b. Đặt . Tính theo và .
B3. Cho DABC. Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng:

B4. Cho DABC có trọng tâm G. Gọi H là điểm đối xứng của B qua G.
