Các Định Nghĩa Liên Quan Vectơ
I. TÓM TẮT LÝ THUYẾT
Các định nghĩa
Vectơ là một đoạn thẳng có hướng. Kí hiệu vectơ có điểm đầu A, điểm cuối B là 
Giá của vectơ là đường thẳng chứa vectơ đó.
Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ, kí hiệu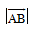 
.
Vectơ – không là vectơ có điểm đầu và điểm cuối trùng nhau, kí hiệu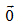 
.
Hai vectơ đgl cùng phương nếu giá của chúng song song hoặc trùng nhau.
Hai vectơ cùng phương có thể cùng hướng hoặc ngược hướng.
Hai vectơ đgl bằng nhau nếu chúng cùng hướng và có cùng độ dài.
Chú ý: + Ta còn sử dụng kí hiệu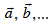 
để biểu diễn vectơ.
+ Qui ước: Vectơ 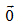cùng phương, cùng hướng với mọi vectơ.
Mọi vectơ 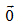đều bằng nhau.
Hệ thức trung điểm đoạn thẳng:
M là trung điểm của đoạn thẳng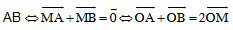 
(O tuỳ ý).
Hệ thức trọng tâm tam giác:
G là trọng tâm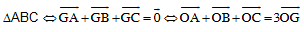 
(O tuỳ ý).
II. PHƯƠNG PHÁP GIẢI BÀI TẬP
VĐ1. Xác định vectơ
B1. (B1-SGK). Cho 3 vectơ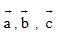 
đều khác vectơ 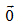, các khẳng định sau đúng hay sau:
a. Nếu 
cùng phương với 
cùng phương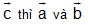
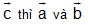b. Nếu cùng ngược hướng với cùng phương
B2. Cho tam ABC.Có thể xác định được bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là các đỉnh A, B, C.
B3. Cho tứ giác ABCD.Có thể xác định được bao nhiêu vectơ (khác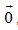 
) có điểm đầu và điểm cuối là các điểm A, B, C, D ?
B4. Cho DABC có A¢, B¢, C¢ lần lượt là trung điểm của các cạnh BC, CA, AB.
a) Chứng minh: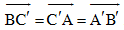 
.
b) Tìm các vectơ bằng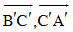 
.
B5. Cho tam giác ABC, xác định vectơ có điểm đầu là A và vectơ ấy cùng phương với cả 2 vectơ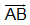 
và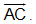 
B6. Cho hình bình hành ABCD có tâm O. Gọi E, F lần lượt là trung điểm BC và CD
a) Xác định vectơ có điểm đầu là E, có độ dài bằng BD/2 và cùng hướng với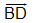 
b) Dựng vectơ có điểm cuối là O, có giá là đường thẳng AC, có độ dài là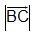 
và ngược hướng với AC.
c) CMR nếu FK có độ dài là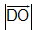 
và ngược hướng với 
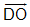thì K thuộc đường thẳng AD.
III. BÀI TẬP ĐỀ NGHỊ
Bài 1.Cho ngũ giác ABCDE. Có thể xác định được bao nhiêu vectơ (khác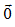 
) có điểm đầu và điểm cuối là các điểm A, B, C, D, E ?
Bài 2. Cho hình bình hành ABCD có tâm là O. Tìm các vecto từ 5 điểm A, B, C, D, O
a. bằng vecto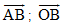 
b. có độ dài bằng 