BÀI 1. BẤT ĐẲNG THỨC
I. TÓM TẮT LÝ THUYẾT
II. PHƯƠNG PHÁP CHỨNG MINH BẤT ĐẲNG THỨC
VẤN ĐỀ 1: Chứng minh BĐT dùng định nghĩa và các tính chất
Để chứng minh một BĐT ta có thể sử dụng các cách sau:
+ Đưa về dạng A- B > 0
+ Biến đổi BĐT cần chứng minh tương đương với một BĐT đúng.
+ Sử dụng một BĐT đúng, biến đổi để dẫn đến BĐT cần chứng minh..
+ Biến đổi vế trái hoặc vế phải
Một số BĐT đúng thường dùng:
i. A2 ≥ 0 ii. A2 + B2 ≥ 0 3i. A.B ≥ 0 với A, B ≥ 0. 4i. A2 + B2 ≥ 2A.B
Chú ý:
– Trong quá trình biến đổi, ta thường chú ý đến các hằng đẳng thức.
– Khi chứng minh BĐT ta thường tìm điều kiện để dấu đẳng thức xảy ra. Khi đó ta có thể tìm GTLN, GTNN của biểu thức.
Bài 1. Chứng minh rằng: 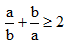 với a, b cùng dấu (tức a.b > 0)
với a, b cùng dấu (tức a.b > 0)
Bài 2. Cho a, b, c, d, e 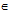 R. Chứng minh các bất đẳng thức sau:
R. Chứng minh các bất đẳng thức sau:
a. a2 + b2 + c2 ≥ ab + bc + ca b. a2 + b2 + 1 ≥ ab + a + b
c. a2 + b2 + c2 + 3 ≥ 2(a + b + c)
Bài 3. Cho a, b, c, d, e 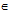 R. Chứng minh các bất đẳng thức sau:
R. Chứng minh các bất đẳng thức sau:
a. a4 + b4 + c2 + 1 ≥ 2a(ab2 – a + c + 1)
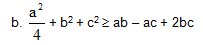
c. a2 + b2 + c2 + d2 + e2 ≥ a(b + c + d + e)
Bài 4. Cho a, b, c  R. Chứng minh các bất đẳng thức sau:
R. Chứng minh các bất đẳng thức sau:
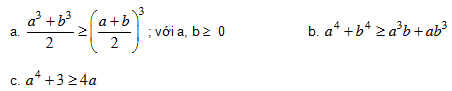
Bài 5. Cho a, b, c, d  R. Chứng minh rằng a2 + b2 ≥ 2ab (1). Áp dụng chứng minh các bất đẳng thức sau:
R. Chứng minh rằng a2 + b2 ≥ 2ab (1). Áp dụng chứng minh các bất đẳng thức sau:
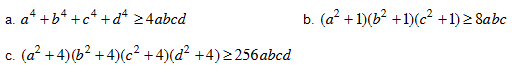
Bài 6. Cho a, b, c, d > 0. Chứng minh rằng nếu 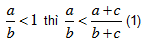 . Áp dụng chứng minh các bất đẳng thức sau:
. Áp dụng chứng minh các bất đẳng thức sau:
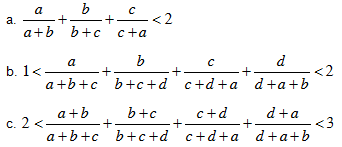
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Cho a, b, c, d, e 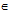 R. Chứng minh bất đẳng thức sau:
R. Chứng minh bất đẳng thức sau:
a2 + b2 + c2 ≥ 2(ab + bc – ca)
HD: BĐT đã cho <=> ( a- b + c)2³ 0
Bài 2. Cho a, b, c, d, e 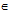 R. Chứng minh bất đẳng thức sau:
R. Chứng minh bất đẳng thức sau:
a2(1 + b2) + b2(1 + c2) + c2(1 + a2) ≥ 6abc
HD: BĐT đã cho <=> ( a – bc)2 + (b – ca)2 + (c – ab)2 ≥ 0
Bài 3. Cho a, b, c 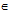 R. Chứng minh các bất đẳng thức sau: a4 + 3 ≥ 4a
R. Chứng minh các bất đẳng thức sau: a4 + 3 ≥ 4a
HD: BĐT đã cho <=> ( a -1)2(a2 + 2a + 3) > 0
Bài 4. Cho a, b, c 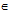 R. Chứng minh bất đẳng thức: a2 + b2 + c2 ≥ ab + bc + ca (1). Áp dụng chứng minh các bất đẳng thức sau:
R. Chứng minh bất đẳng thức: a2 + b2 + c2 ≥ ab + bc + ca (1). Áp dụng chứng minh các bất đẳng thức sau:
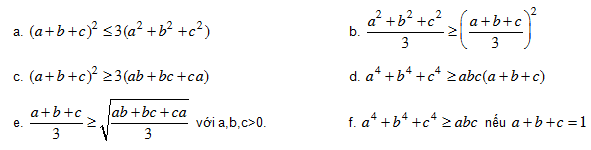
HD: (a – b)2 + (b – c)2 + (c – a)2 ≥ 0.
a. Khai triển, rút gọn, đưa về (1) b, c. Vận dụng a
d. Sử dụng (1) hai lần e. Bình phương 2 vế, sử dụng (1)
f. Sử dụng d)