BÀI 2. BẤT ĐẲNG THỨC CÔ SI
I. TÓM TẮT LÝ THUYẾT
1. Một số bất đẳng thức thông dụng
2. Bất đẳng thức Cô–si:
VẤN ĐỀ: Chứng minh BĐT bằng cách sử dụng BĐT Cô–si
Bài 1. Cho a, b, c ³ 0. Chứng minh các bất đẳng thức sau:
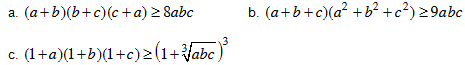
Bài 2. Cho a, b, c ³ 0. Chứng minh các bất đẳng thức sau:
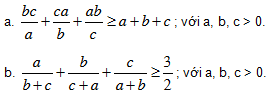
Bài 3. Cho a, b, c > 0. Chứng minh các bất đẳng thức sau:
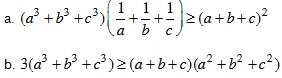
Bài 4. Cho a, b > 0. Chứng minh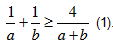 
. Áp dụng chứng minh các BĐT sau:
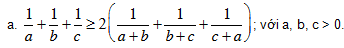
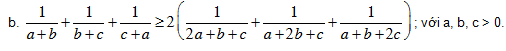
c. Cho a, b, c > 0 thoả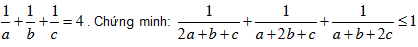 
Bài 5. Cho a, b, c > 0. Chứng minh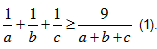 
. Áp dụng chứng minh các BĐT sau:
.
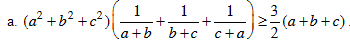b. Cho x, y, z > 0 thoả x + y + z = 1. Tìm GTLN của biểu thức: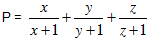 
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Cho a, b, c ³ 0. Chứng minh các bất đẳng thức sau:
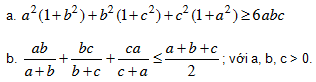
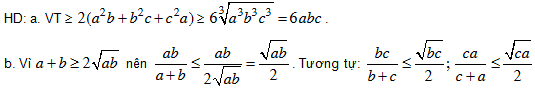
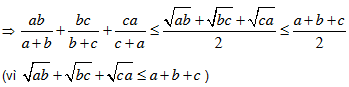
Bài 2. Cho a, b, c > 0. Chứng minh các bất đẳng thức sau: 9(a3 + b3 + c3) ³ (a + b + c)3
HD: Áp dụng bài 3b) ta có: 9(a3 + b3 + c3) ³ 3(a + b + c)(a2 + b2 + c2)
Từ đó ta được: 3(a2 + b2 + c2) ³ (a + b + c)2 Þ đpcm.
Bài 3. Cho a, b > 0. Chứng minh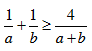 
(1). Áp dụng chứng minh các BĐT sau:
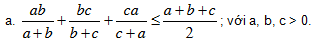
b. Cho x, y, z > 0 thoả x + 2y + 4z = 12. Chứng minh: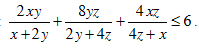 
c. Cho a, b, c là độ dài ba cạnh của một tam giác, p là nửa chu vi. Chứng minh rằng:
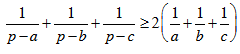
HD a. Theo (1):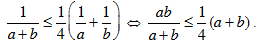 
Cùng với các BĐT tương tự, cộng vế theo vế ta được đpcm.
b. Áp dụng câu d) với a = x, b = 2y, c = 4z thì a + b + c = 12 Þ đpcm.
c. Nhận xét: (p –a) + (p – b) = 2p – (a + b) = c.
Áp dụng (1) ta được: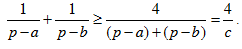 
Cùng với 2 BĐT tương tự, cộng vế theo vế, ta được đpcm.