BÀI 3. BẤT ĐẲNG THỨC CHỨA GIÁ TRỊ TUYỆT ĐỐI
I. TÓM TẮT LÝ THUYẾT
1. Bất đẳng thức về giá trị tuyệt đối
2. Bất đẳng thức về các cạnh của tam giác
II. BÀI TẬP ÁP DỤNG
Bài 1. Cho a, b, c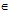 
R. Chứng minh các bất đẳng thức sau:
a. |a – b| ≤ |a – c| + | c – b|
b. |a ± b| ≥ |a| – |b|
Bài 2. Chứng minh rằng nếu: |a| + |b| = a + b thì a, b ≥ 0.
Bài 3. Bài 10 – Trang 110 – SGK – Đại số 10 – Nâng cao
a. Chứng minh rằng nếu x ≥ y ≥ 0 thì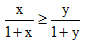 
b. Chứng minh rằng đối với hai số tùy ý a, b ta có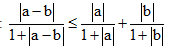 
Đẳng thức xảy ra khi nào?
Bài 4. B2 – Trang 109 – SGK – Đại số 10 – Nâng cao
Chứng minh rằng nửa chu vi của một tam giác lớn hơn độ dài mỗi cạnh của tam giác đó
Bài 5. (Bài 3 – Trang 79 – SGK – Đại số 10 – Cơ bản)
Cho a, b, c là độ dài ba cạnh của một tam giác.
a) Chứng minh (b – c)2 < a2
b) Từ đó suy ra a2 + b2 + c2 < 2(ab + bc + ca)
Bài 6. Cho a, b, c là độ dài 3 cạnh của một tam giác. Chứng minh:
a. ab + bc + ca ≤ a2 + b2 + c2 < 2(ab + bc + ca)
b. abc ≥ ( a + b – c)( b + c – a)(a + c – b)
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Cho a, b, c là độ dài 3 cạnh của một tam giác. Chứng minh:
2a2b2 + 2b2c2 + 2c2a2 – a4 – b4 – c4 > 0
HD: BĐT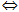 
(a + b + c)(a + b – c)(b + c – a)(c + a – b) > 0.
Bài 2. Cho a, b, c là độ dài 3 cạnh của một tam giác. Chứng minh:
a(b – c)2 + b(c – a)2 + c(a + b)2 > a3 + b3 + c3
HD: BĐT 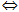(a + b – c)(b + c – a)(c + a – b) > 0.