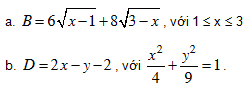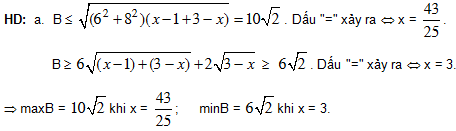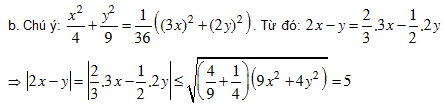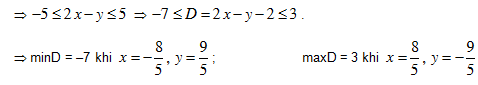BÀI 6. ỨNG DỤNG BẤT ĐẲNG THỨC ĐỂ TÌM GTLN-GTNN (nâng cao)
I. TÓM TẮT LÝ THUYẾT
Tìm GTLN của một tích: A.B
+ Kiểm tra A, B > 0: A + B = const
+ Tích A.B đạt GTLN khi và chỉ khi A = B
Tìm GTNN của một tổng: A + B
+ Kiểm tra A, B > 0: A.B = const
+ Tổng A + B đạt GTNN khi và chỉ khi A = B
Sử dụng điều kiện dấu bằng xảy ra của BĐT thông dụng, BĐT Cô-si, Bu-nhi-cốp-ski,..
Lưu ý: GTLN, GTNN phải đạt được khi có dấu “=” xảy ra
II. BÀI TẬP ÁP DỤNG
Bài 1. Cho ba số a, b, c thỏa mãn điều kiện ab + bc + ca =1. Tìm GTNN của biểu thức A = a2 + b2 + c2
Bài 2. Cho 2x + 5y = 7. Tìm GTNN của M = 2x2 + 5y2 + 2006
Bài 3. Cho x, y, z là ba số dương và x + y + z = 1. Tìm giá trị lớn nhất của biểu thức:
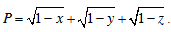
Bài 4. Cho x, y > 0. Tìm GTNN của các biểu thức sau:

Bài 5. Tìm GTLN của các biểu thức sau:

Bài 6. Tìm GTLN, GTNN của các biểu thức sau:
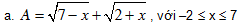
b. C = y – 2x + 5, với 36x2 + 16y2 = 9.
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Tìm GTLN, GTNN của các biểu thức sau: