BÀI 3 : ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG
Bài 1. Cho tứ diện đều ABCD. Chứng minh các cặp cạnh đối diện của tứ diện này vuông góc với nhau từng đôi một, nghĩa là cần chứng minh AB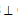 
CD, BC 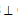AD, AC 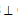BD.
Bài 2. Hình chóp S.ABCD có cạnh SA vuông góc với mặt phẳng (ABCD) và đáy ABCD là hình thang vuông tại A và D với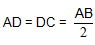 
.
a. Gọi I là trung điểm của đoạn AB, chứng minh CI 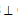AB và DI 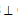SC.
b. Chứng minh các mặt bên của hình chóp S.ABCD là các tam giác vuông.
Bài 3. Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Cạnh bên CC’ vuông góc với đáy và CC’ = a.
a. Gọi I là trung điểm của BC. Chứng minh AI 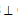BC’.
b. Gọi M là trung điểm của BB’. Chứng minh BC’ 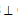AM.
c. Gọi K là điểm trên đoạn A’B’ sao cho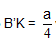 
và J là trung điểm của B’C’. Chứng minh rằng : AM 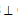MK và AM 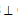KJ.
Bài 4. Cho góc vuông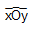 
nằm trong mặt phẳng 
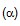. Trên đường thẳng Oz vuông góc với mặt phẳng 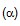tại O lấy một điểm C, trên đường thẳng Ox lấy điểm A và trên đường thẳng Oy lấy điểm B.
a. Chứng minh tứ diện OABC có ba cặp cạnh đối diện vuông góc với nhau.
b. Gọi H là hình chiếu vuông góc của điểm O trên mặt phẳng (ABC). Chứng minh H là trực tâm của tam giác ABC.
c. Chứng minh rằng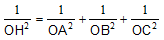 
Bài 5. Cho hình chóp S.ABCD có cạnh SA vuông góc với mặt phẳng (ABCD) và đáy ABCD là hình thang vuông tại A và D với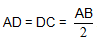 
. Gọi I là trung điểm của AB.
a. Chứng minh CI 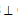SB và DI 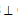SC.
b. Chứng minh các mặt bên của hình chóp S.ABCD là các tam giác vuông.