TÍCH CỦA VECTO VỚI MỘT SỐ
I. TÓM TẮT LÝ THUYẾT
Tích của một vectơ với một số
Cho vectơ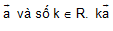 
và số k Î R. là một vectơ được xác định như sau:
+ 
ngược hướng với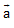 
nếu k < 0.
+ 
.
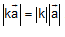Tính chất: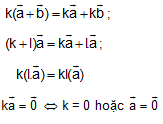
Điều kiện để hai vectơ cùng phương: 
Điều kiện ba điểm thẳng hàng: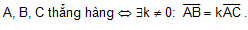 
Biểu thị một vectơ theo hai vectơ không cùng phương: Cho hai vectơ không cùng phương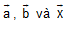 
tuỳ ý. Khi đó 
.
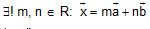II. PP GIẢI BÀI TẬP
B1: CMR I là trung điểm đoạn AB khi và chỉ khi với điểm M bất kỳ, ta có: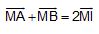
B2: Cho tam giác ABC với trọng tâm G. Chứng minh rằng với M bất kỳ ta có: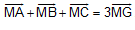
.
B3.Cho hai tam giác ABC và A¢B¢C¢ lần lượt có các trọng tâm là G và G¢.
a. Chứng minh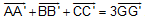 
.
b. Từ đó suy ra điều kiện cần và đủ để hai tam giác có cùng trọng tâm.
B4. Cho tam giác ABC. Trên các cạnh AB, BC, CA lấy lần lượt các điểm M, N, P sao cho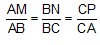 
. CMR hai tam giác ABC và MNP có cùng trọng tâm.
B5. Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD và O là trung điểm của EF. M là một điểm tùy ý. CMR:
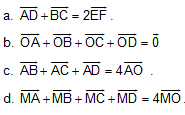
B6. Cho tam giác ABC có G là trọng tâm. Trên cạnh BC lấy điểm A’ sao cho: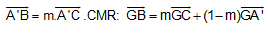
B7: Cho tam giác ABC vuông tai A có Ab = 3a, AC = 4a. Gọi H là chân đường cao hạ từ A xuống BC. Ta đặt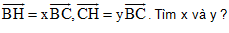 
III. BÀI TẬP ĐỀ NGHỊ
B1: Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3 CM, trên đoạn Am lấy N sao cho 2AN = 5MN.
Đặt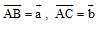 
a. Phân tích các vecto 
b. Gọi I là giao điểm của BN và AC. Tính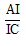 
B2: Cho tam giác ABC trọng tâm G, Gọi I là trung điểm đoạn AG và K là trung điểm trên cạnh AB sao cho AK = 0,2 AB. Hãy phân tích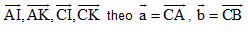 
B3: Cho tam giác ABC, M là một điểm nằm trên cạnh BC. CMR 