BÀI 1. PHƯƠNG TRÌNH ĐƯỜNG THẲNG
I. TÓM TẮT LÝ THUYẾT
1. Vectơ chỉ phương của đường thẳng
Vectơ 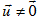 được gọi là vectơ chỉ phương của đường thẳng
được gọi là vectơ chỉ phương của đường thẳng 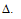 nếu giá của nó song song hoặc trùng với
nếu giá của nó song song hoặc trùng với
Nhận xét:
– 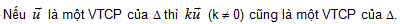
– Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một VTCP.
2. Phương trình tham số của đường thẳng
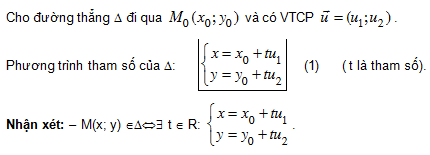

3. Phương trình chính tắc của đường thẳng
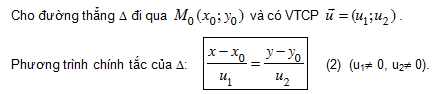
Chú ý: Trong trường hợp u1 = 0 hoặc u2 = 0 thì đường thẳng song song với trục tọa độ và không có phương trình chính tắc.
II. BÀI TẬP ÁP DỤNG
Bài 1. Lập PTTS, PTCT (nếu có), hệ số góc (nếu có) của các đường thẳng đi qua điểm M và có VTCP 

Bài 2. Lập PTTS, PTCT (nếu có), hệ số góc (nếu có) của các đường thẳng đi qua điểm M và có VTCP

Bài 3. Lập PTTS, PTCT (nếu có), hệ số góc (nếu có) của các đường thẳng đi qua điểm M và có VTCP

Bài 4. Lập PTTS, PTCT (nếu có) của các đường thẳng đi qua điểm M và có hệ số góc k:
a. M(–2; 1), k = –2 b. M(–2; 4), k = 3
c. M º O(0; 0), k = 4
Bài 5. Lập PTTS, PTCT (nếu có), hệ số góc (nếu có) của các đường thẳng đi qua hai điểm A, B:
a. A(–2; 3), B(1; 3) b. A(4; 0), B(3; 0)
c. A(0; 3), B(0; –2)
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Lập PTTS, PTCT (nếu có) của các đường thẳng đi qua điểm M và có hệ số góc k:
a. M(5; 2), k = 1 b. M(–3; –4), k = –1
c. M(2; –4), k = 0
Bài 2. Lập PTTS, PTCT (nếu có), hệ số góc (nếu có) của các đường thẳng đi qua điểm M và có VTCP

Bài 3. Lập PTTS, PTCT (nếu có), hệ số góc (nếu có) của các đường thẳng đi qua điểm M và có VTPT

