XÁC ĐỊNH MẶT TRỤ – HÌNH TRỤ – KHỐI TRỤ
I. TÓM TẮT LÝ THUYẾT
1. Mặt trụ
Mặt trụ là hình tròn xoay sinh bởi đường thẳng l khi xoay quanh đường thẳng D song song và cách l một khoảng R. D được gọi là trục, R gọi là bán kính, l gọi là đường sinh
Định nghĩa khác, mặt trụ là tập hợp tất cả những điểm cách đường thẳng D cố định một khoảng R không đổi.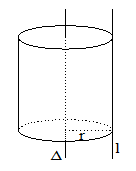
2. Hình trụ
Hình trụ là hình giới bạn bởi mặt trụ và hai đường tròn bằng nhau, là giao tuyến của mặt trụ và 2 mặt phẳng vuông góc với trục.
Hình trụ là hình tròn xoay khi sinh bởi bốn cạnh của hình một hình chữ nhật khi quay xung quanh một đường trung bình của hình chữ nhật đó.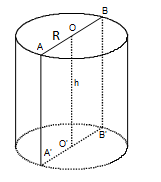
Diện tích xung quanh của hình trụ:
Sxq = 2π.R.l
Diện tích toàn phần hình trụ:
Stp = 2π.R.l+2π.R2
3. Khối trụ
Khối trụ là hình trụ cùng với phần bên trong của hình trụ đó.
Thể tích khối trụ tròn xoay có bán kính R và đường cao h là: V = pR2.h.
II. PHƯƠNG PHÁP GIẢI BÀI TẬP
Bài 1: Hãy tìm hình tạo bởi giao của một mặt phẳng (P) song song với trục của hình trụ. Từ đó, xác định vị trí của mặt phẳng (P) để thiết diện của nó có diện tích lớn.
Bài 2. Cho đường tròn (O;R) nằm trong mặt phẳng (P). Tìm tập hợp các điểm M trong không gian sao cho hình chiếu của chúng trên (P) luôn nằm trên đường tròn đã cho.
Bài 3: Cho hai điểm A, B cố định, AB = a. Tìm tập hợp những điểm M trong không gian sao cho diện tích tam giác MAB bằng S không đổi.
Bài 4: Cho mặt phẳng α, một điểm A nằm trên α, một điểm B nằm ngoài α sao cho hình chiếu vuông góc H của B trên α không trùng với A. Một điểm M chạy trong α sao cho luôn luôn có ∠ABM = ∠BMH. Tìm tập hợp điểm M.
Bài 5. Cho hình trụ có bán kính R và chiều cao cũng bằng R. Một hình vuông ABCD có hai cạnh AB và CD lần lượt là dây cung của hai đường tròn đáy, các cạnh AD và BC không phải là đường sinh của hình tròn. Tính cạnh của hình vuông đó.
III. BÀI TẬP TƯƠNG TỰ
Bài 1: Cho đường tròn (O; R) nằm trong mặt phẳng (P). Tìm tập hợp các điểm M trong không gian sao cho hình chiếu của chúng trên (P) luôn nằm trên đường tròn đã cho.
Bài 2: Cho điểm A cố định và nằm ngoài đường thẳng d cố định. Một đường thẳng a thay đổi nhưng luôn vuông góc với d và cắt d. Tìm tập hợp các điểm M là hình chiếu A lên a.
Bài 3: Trên hai đáy của hình trụ có đường cao gấp đôi bán kính đáy, ta lấy hai bán kính chéo nhau, đông thời tạo với nhau một góc là 300 . Biết rằng đoạn thẳng nối hai đầu mút của hai bán kính không đi qua tâm đường tròn có độ dài là a. Tính tan của góc hợp trục và đoạn thẳng qua 2 mút đó.
Bài 4. Cho hình trụ có bán kính R và đường RÖ2. Gọi AB và CD là hai đường kính thay đổi của hai đường tròn đáy mà AB vuông góc với CD.
a. Chứng minh rằng ABCD là tứ diện đều.
b. Chứng minh rằng các đường thẳng AC, AD, BC, BD luôn tiếp xúc với một mặt trụ cố định.