BÀI. PHÉP VỊ TỰ
I. TÓM TẮT LÝ THUYẾT
1. Định nghĩa:
2. Tính chất: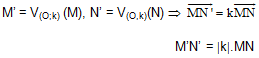
Ba đường thẳng hàng 
3 điểm thẳng hàng và bảo toàn thứ tự.
Đường thẳng đường thẳng song song hoặc trùng với nó.
Tia tia, góc 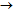góc bằng chính nó.
Tam giác 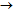D đồng dạng
Đường tròn bán kính R thành đường tròn có bán kính R’ = |k|.R
3. Biểu thức tọa độ: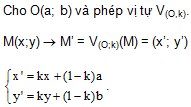
II. PHƯƠNG PHÁP GIẢI BÀI TẬP
VĐ 1: Tìm ảnh của phép vị tự.
Phương pháp: dùng định nghĩa phép vị tự, dùng biểu thức tọa độ
B1: Cho DABC có 3 góc nhọn và H là trực tâm
Bài 1 – SGK. Tìm ảnh của tam giác ABC qua V(H; 1/2).
Bài 2. Cho DOMN. Dựng ảnh của M, N qua phép vị tự tâm O, tỉ số k trong mỗi trường hợp sau:
a. k = 3 b. k = 1/2 c. k = -3/4 .
Bài 3. Tìm ảnh của các điểm sau qua phép vị tự tâm O
a. A(1; 2) O(3; -1) k = 2 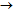A’(-1; 5)
b. B(2; -4) O(-1; 2) k = -2 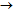B’(-7; 14)
c. C(8; 3) O(2; 1) k =1/2 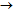C’(5; 2)
Bài 4. Trong mặt phẳng Oxy, cho d: 2x + y – 4 = 0. Hãy viết phương trình của d’ là ảnh của d qu phép vị tự tâm O(0;0) tỉ số k = 3.
Bài 5. Trong mặt phẳng Oxy: (C ): (x – 3)2 + (y + 1)2 = 9 , k = -2. Tìm (C’) là ảnh của (C ) qua V(I; -2) với f (1; 2)
III. BÀI TẬP ĐỀ NGHỊ
Bài 1: Cho ba điểm A(-1; 2), B(3; 1), C(-1; 5). Tồn tại hay không tồn tại một phép vị tự tâm A, tỉ số k biến B thành C.
Hướng dẫn giải.
Giả sử tồn tại một phép vị tự tâm A, tỉ số k biến B thành C
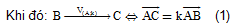
Bài 2: Cho DABC có AB = 4, AC = 6, AD là phân giác trong của ΔABC của DABC (D
BC). Với giá trị nào của k thì phép vị tự tâm D, tỉ số k biến B thành C
Hướng dẫn giải
Bài 3. Cho DABC có hai đỉnh là B và C cố định, còn đỉnh A di động trên đường tròn (C ) cho trước. Tìm tập hợp các trọng tâm của DABC.
Đáp án
Tập hợp G là đường tròn (O’), đó chính là ảnh của đường tròn (O) qua phép vị tự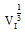 
.
Bài 4. Tìm phép vị tự biến d thành d’
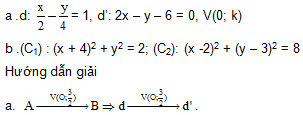
b. Có hai phép vị tự biến (C1) 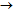(C2) là V(I; -2) với I(-2; 1) hoặc V(I; 2) với I(-10; -3)
Bài 5. Cho đường tròn (O; R) đường kính AB. Một đường tròn (O’) tiếp xúc với (O; R) và đoạn AB tại C, D, đường thẳng CD cắt (O; R) tại I. Chứng minh rằng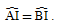 
.
Hướng dẫn giải
C là tâm vị tự của hai đường tròn (O) và (O’)
D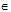
(O’), I 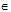(O) và ba điểm C, D, I thẳng hàng
Gọi R’ là bán kính của đường tròn (O’), khi đó:
Bài 6. Cho hai đường tròn (O1; R1) và (O2; R2) ngoài nhau R1¹ R2. Một đường tròn (O) thay đổi tiếp xúc ngoài với (O1) tại A tiếp xúc ngoài với (O2) tại B. Chứng minh rằng : đường thẳng AB luôn luôn đi qua một điểm cố định.
Hướng dẫn giải