BÀI 9. LẬP PHƯƠNG TRÌNH ĐƯỜNG TRÒN (P1)
Để lập phương trình đường tròn (C) ta thường cần phải xác định tâmI (a; b) và bán kính R của (C). Khi đó phương trình đường tròn (C) là:
(x – a)2 + (y – b)2 = R2.
Dạng 1: (C) có tâm I và đi qua điểm A.
– Bán kính R = IA.
Dạng 2: (C) có tâm I và tiếp xúc với các trục tọa độ
– Tâm I có một tọa độ bằng 0.
Dạng 3: (C) có đường kính AB.
– Tâm I là trung điểm của AB.
– Bán kính 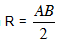 .
.
II. BÀI TẬP ÁP DỤNG
Bài 1. Viết phương trình đường tròn có tâm I và đi qua điểm A, với: (dạng 1)
a. I(2; 4), A(–1; 3) b. I(–3; 2), A(1; –1)
Bài 2. Tìm phương trình của đường tròn có tâm là gốc tọa độ và đi qua điểm A(3, 2).
Bài 3. Tìm phương trình của đường tròn có tâm I(4, 2) và tiếp xúc với trục Ox.
Bài 4. Tìm phương trình của đường tròn có tâm I(–5, –2) và tiếp xúc với trục Oy.
Bài 5. Viết phương trình đường tròn tâm I(2, 3) và đi qua gốc tọa độ O.
Bài 6. Viết phương trình đường tròn đường kính AB với: A(2, 3); B(4, 7).
Dạng 4: (C) đi qua ba điểm không thẳng hàng A, B, C (đường tròn ngoại tiếp tam giác).
Cách 1:
– Phương trình của (C) có dạng: x2 + y2 + 2ax + 2by + c = 0 (*).
– Lần lượt thay toạ độ của A, B, C vào (*) ta được hệ phương trình.
– Giải hệ phương trình này ta tìm được a, b, c Þ phương trình của (C).
Cách 2:
– Tâm I của (C) thoả mãn: 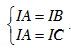 .
.
– Bán kính R = IA = IB = IC.
Bài 7. Tìm phương trình của đường tròn qua ba điểm A(2, 0); B(0, 1); C(–1, 2)
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Viết phương trình đường tròn có tâm I và đi qua điểm A, với:
a. I(–1; 0), A(3; –11) b. I(1; 2), A(5; 2)
Bài 2. Viết phương trình đường tròn có tâm I và tiếp xúc với đường thẳng D, với:

Bài 3. Viết phương trình đường tròn có đường kính AB, với:
a. A(0; 1), C(5; 1) b. A(–3; 4), B(7; 2)
Bài 4. Viết phương trình đường tròn ngoại tiếp tam giác ABC, với:
a. A(2; 0), B(0; –3), C(5; –3) b. A(5; 3), B(6; 2), C(3; –1)