BÀI 5. GÓC GIỮA HAI ĐƯỜNG THẲNG
I. TÓM TẮT LÝ THUYẾT
Góc giữa hai đường thẳng
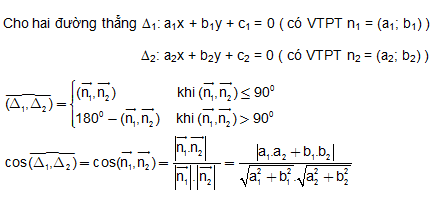
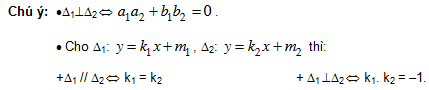
II. BÀI TẬP ÁP DỤNG
Bài 1. Tìm góc giữa hai đường thẳng trong mỗi trường hợp sau:
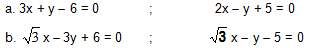
Bài 2. Tính góc giữa hai đường thẳng:
a. 2x – y + 5 = 0, 3x + y – 6 = 0
b. 3x – 7y + 26 = 0, 2x + 5y – 13 = 0.
Bài 3. Tính số đo của các góc trong tam giác ABC, với:
a. A(1; 2), B(5; 2), C(1; –3)
b. AB: 2x – 3y + 21 = 0, BC: 2x + 3y + 9 = 0, CA: 3x – 2y – 6 = 0
Bài 4. Viết phương trình đường thẳng đi qua M(2, 5) và hợp với đường x – 3y + 6 = 0 một góc bằng 450.
Bài 5. Cho hai điểm A(3, 3) và B(0, 2). Tìm trên đường thẳng: x + y – 4 = 0 một điểm nhìn đoạn AB dưới một góc 450.
Bài 6. Cho hai đường thẳng  . Tìm m để góc giữa hai đường thẳng đó
. Tìm m để góc giữa hai đường thẳng đó  , với:
, với:
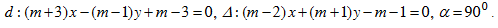
Bài 7. Một tam giác cân có cạnh đáy và cạnh bên theo thứ tự được xác định bởi các phương trình: x + y – 1 = 0 và 2x – y + 1 = 0. Tìm phương trình của cạnh còn lại, biết rằng nó đi qua điểm M(–1, 2).
Bài 8. Tìm phương trình cạnh góc vuông của một tam giác vuông cân, biết rằng phương trình cạnh huyền là: 2x + y – 1 = 0 và đỉnh góc vuông là A(2, 3)
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Tính góc giữa hai đường thẳng:
a. x – 2y – 1 = 0, x + 3y – 11 = 0
b. 3x + 4y – 5 = 0, 4x – 3y + 11 = 0
Bài 2. Tính số đo của các góc trong tam giác ABC, với:
a. A(–3; –5), B(4; –6), C(3; 1)
b. AB: 4x + 3y + 12 = 0, BC: 3x – 4y – 24 = 0, CA: 3x + 4y – 6 = 0
Bài 3. Viết phương trình đường thẳng d đi qua điểm A và tạo với đường thẳng D một góc a, với:
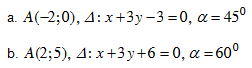
Bài 4. Cho hai đường thẳng  . Tìm m để góc giữa hai đường thẳng đó
. Tìm m để góc giữa hai đường thẳng đó  , với:
, với:
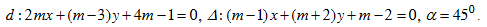
Bài 5. Cho hình vuông ABCD có tâm I(4; –1) và phương trình một cạnh là .
a. Viết phương trình hai đường chéo của hình vuông.
b. Tìm toạ độ 4 đỉnh của hình vuông.