GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC BẤT KỲ
1. Định nghĩa
Lấy M trên nửa đường tròn đơn vị tâm O. Xét góc nhọn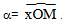 
. Giả sử M(x; y).
sina = y (tung độ)
cosa = x (hoành độ)
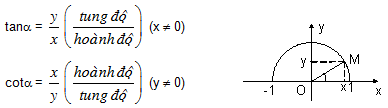
Chú ý
– Nếu a t thì cosa< 0, tana< 0, cota< 0.
– tana chỉ xác định khi a¹ 900, cota chỉ xác định khi a¹ 00 v a¹ 1800.
2. Tính chất
- · Góc phụ nhau · Góc bù nhau
sin(900 – a) = cosa sin(1800 – a) = sina
cos(900 – a) = sina cos(1800 – a) = -cosa
tan(900 – a) = cota tan(1800 – a) = – tana
cot(900 – a) = tana cot(900 – a) = – cota
3. Giá trị lượng giác của các góc đặc biệt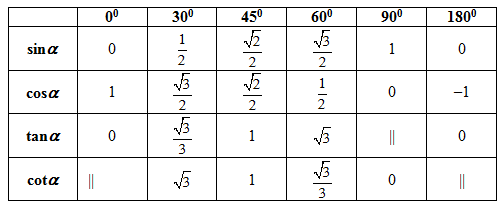
4. Các hệ thức cơ bản
Chú ý: 0 £ sina £1; -1£cosa£1.
PP GIẢI BÀI TẬP
Bài 1. Tính giá trị các biểu thức sau:
a. asin00 + bcos00 + csin900.
b. acos900 + bsin90 + csin1800.
c. a2sin900 + b2cos900 + c2cos1800.
d. 3 – sin2900 + 2cos2600 – 3tan2450.
e. 4a2sin2450 – 3(atan450)2 + (2acos450)2.
Bài 2. (B1-SGK) CMR trong tam gic ABC ta có:
a. sinA = sin(B+C); b. cosA = – cos(B+C)
Bài 3. (B2-SGK) CMR:
a. sin1050 = sin750
b. cos1700= – cos100
c. cos1220 = – cos580
Bài 4. Tính giá trị của các biểu thức sau:
a. sinx + cosx khi x bằng 00; 450; 600.
b. 2sinx + cos2x khi x bằng 450; 300.
Bài 5. Cho biết một giá trị lượng giác của một góc, tính các giá trị lượng giác còn lại: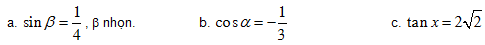
Bài 6. (B5 –SGK HH12) Cho góc x, với cosx=1/3. Tính giá trị của biểu thức:
P = 3 sin2x + cos2x.
BÀI TẬP ĐỀ NGHỊ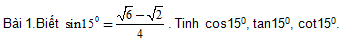
Bài 2. Chứng minh các đẳng thức sau:
a. (sinx + cosx)2 = 1 + 2sinx.cosx
b. sin4x + cos4x = 1 – 2sin2x.cos2x.
c. tan2x – sin2x = tan2x.sin2x.
d. sin6x + cos6x = 1 – 3sin2x.cos2x
Bài 3. Đơn giản các biểu thức sau:
a. cosy + siny.tany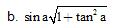
c. sin(900 – x) + cos(1800 – x) + sin2x(1 + tan2x) – tan2x.
Bài 4. Cho góc x nhọn với cosx = 1/4, Tính các giá trị lượng giác của các góc x.